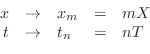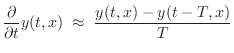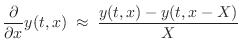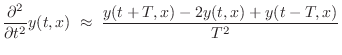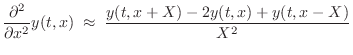DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Finite-Difference Schemes

Finite-Difference Schemes (FDSs) aim to solve differential equations by means of finite differences. For example, as discussed in §C.2, if $ y(t,x)$ denotes the displacement in meters of a vibrating string at time $ t$ seconds and position $ x$ meters, we may approximate the first- and second-order partial derivatives by

$\displaystyle {\dot y}(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial}{\partial t}y(t,x) \;\approx\; \frac{y(t,x)-y(t-T,x)}{T}$  
$\displaystyle y'(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial}{\partial x}y(t,x) \;\approx\; \frac{y(t,x)-y(t,x-X)}{X}$  
$\displaystyle {\ddot y}(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial^2}{\partial t^2} y(t,x) \;\approx\; \frac{y(t+T,x) - 2 y(t,x) + y(t-T,x) }{T^2}$  
$\displaystyle y''(t,x)$ $\displaystyle \isdef$ $\displaystyle \frac{\partial^2}{\partial x^2} y(t,x) \;\approx\; \frac{y(t,x+X) - 2 y(t,x) + y(t,x-X) }{X^2} \protect$ (D.1)

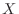
where $ T$ denotes the time sampling interval and $ X$ denotes the spatial sampling interval. Other types of finite-difference schemes were derived in Chapter 7 (§7.3.1), including a look at frequency-domain properties. These finite-difference approximations to the partial derivatives may be used to compute solutions of differential equations on a discrete grid:

\begin{displaymath} \begin{array}{rclcl} x &\to& x_m&=& mX\nonumber \\ t &\to& t_n&=& nT\nonumber \end{array}\end{displaymath}

Let us define an abbreviated notation for the grid variables

$\displaystyle y_{n,m}\isdef y(nT,mX) $

and consider the ideal string wave equation (cf, §C.1):

$\displaystyle y''= \frac{1}{c^2}{\ddot y} \protect$ (D.2)

where $ c$ is a positive real constant (which turns out to be wave propagation speed). Then, as derived in §C.2, setting $ X=cT$ and substituting the finite-difference approximations into the ideal wave equation leads to the relation

$\displaystyle y_{n+1,m}+ y_{n-1,m}= y_{n,m+1}+ y_{n,m-1} $

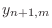
everywhere on the time-space grid (i.e., for all $ n$ and $ m$). Solving for $ y_{n+1,m}$ in terms of displacement samples at earlier times yields an explicit finite-difference scheme for string displacement:

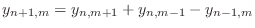$\displaystyle y_{n+1,m}= y_{n,m+1}+ y_{n,m-1}- y_{n-1,m} \protect$ (D.3)

The FDS is called explicit because it was possible to solve for the state at time $ n$ as a function of the state at earlier times (and any other positions $ m$). This allows it to be implemented as a time recursion (or ``digital filter'') which computes a solution at time $ n$ from solution samples at earlier times (and any spatial positions). When an explicit FDS is not possible (e.g., a non-causal filter is derived), the discretized differential equation is said to define an implicit FDS. An implicit FDS can often be converted to an explicit FDS by a rotation of coordinates [55,481].

Next Section:
Convergence
Previous Section:
Non-Cylindrical Acoustic Tubes