Horizontal and Vertical Transverse Waves
The transverse waves considered up to now represent string vibration
only in a single two-dimensional plane. One such plane can be chosen
as being perpendicular to the top plate of a stringed musical instrument. We
will call this the ![]() plane and refer to it as the vertical
plane of polarization for transverse waves on a string (or simply the
vertical component of the transverse vibration). To more fully
model a real vibrating string, we also need to include transverse waves
in the
plane and refer to it as the vertical
plane of polarization for transverse waves on a string (or simply the
vertical component of the transverse vibration). To more fully
model a real vibrating string, we also need to include transverse waves
in the ![]() plane, i.e., a horizontal plane of polarization (or
horizontal component of vibration). Any polarization for transverse
traveling waves can be represented as a linear combination of
horizontal and vertical polarizations, and general transverse string
vibration in 3D can be expressed as a linear superposition of
vibration in any two distinct polarizations.
plane, i.e., a horizontal plane of polarization (or
horizontal component of vibration). Any polarization for transverse
traveling waves can be represented as a linear combination of
horizontal and vertical polarizations, and general transverse string
vibration in 3D can be expressed as a linear superposition of
vibration in any two distinct polarizations.
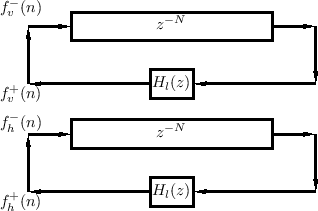 |
If string terminations were perfectly rigid, the horizontal polarization would be largely independent of the vertical polarization, and an accurate model would consist of two identical, uncoupled, filtered delay loops (FDL), as depicted in Fig.6.19. One FDL models vertical force waves while the other models horizontal force waves. This model neglects the small degree of nonlinear coupling between horizontal and vertical traveling waves along the length of the string--valid when the string slope is much less than unity (see §B.6).
Note that the model for two orthogonal planes of vibration on a single string is identical to that for a single plane of vibration on two different strings.
Next Section:
Coupled Horizontal and Vertical Waves
Previous Section:
EDR-Based Loop-Filter Design



















