DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Coupled Horizontal and Vertical Waves

No vibrating string in musical acoustics is truly rigidly terminated, because such a string would produce no sound through the body of the instrument.7.15Yielding terminations result in coupling of the horizontal and vertical planes of vibration. In typical acoustic stringed instruments, nearly all of this coupling takes place at the bridge of the instrument.

Figure 6.20: Digital waveguide model of a string in which vertical and horizontal planes of vibration are coupled linearly at the bridge.
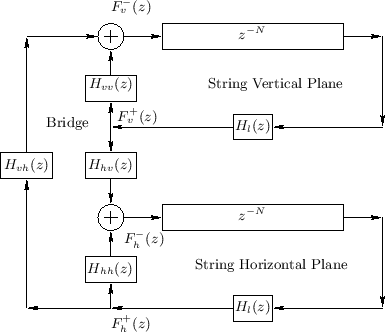\includegraphics{eps/fdlscoupled}

Figure 6.20 illustrates the more realistic case of two planes of vibration which are linearly coupled at one end of the string (the ``bridge''). Denoting the traveling force waves entering the bridge from the vertical and horizontal vibration components by $ F_v^+(z)$ and $ F_h^+(z)$, respectively, the outgoing waves in each plane are given by

$\displaystyle \left[\begin{array}{c} F_v^-(z) \\ [2pt] F_h^-(z) \end{array}\rig... ...] \left[\begin{array}{c} F_v^+(z) \\ [2pt] F_h^+(z) \end{array}\right] \protect$ (7.16)

as shown in the figure.

In physically symmetric situations, we expect $ H_{vh}(z) = H_{hv}(z)$. That is, the transfer function from horizontal to vertical waves is normally the same as the transfer function from vertical to horizontal waves.

If we consider a single frequency $ \omega $, then the coupling matrix with $ z = e^{j\omega T}$ is a constant (generally complex) matrix (where $ T$ denotes the sampling interval as usual). An eigenanalysis of this matrix gives information about the modes of the coupled system and the damping and tuning of these modes [543].

As a simple example, suppose the coupling matrix $ \mathbf{H}(e^{j\omega T})$ at some frequency has the form

$\displaystyle \mathbf{H}(e^{j\omega T}) = \left[\begin{array}{cc} A & B \\ [2pt] B & A \end{array}\right] $

where $ A$ and $ B$ are any complex numbers. This means both string terminations are identical, and the coupling is symmetric (the simplest case in practice). The eigenvectors are easily calculated to be7.16

$\displaystyle \underline{e}_1 = \left[\begin{array}{c} 1 \\ [2pt] 1 \end{array}... ...uad \underline{e}_2 = \left[\begin{array}{c} 1 \\ [2pt] -1 \end{array}\right], $

and the eigenvalues are $ A+B$ and $ A-B$, respectively.

The eigenvector $ \underline{e}_T=[1, 1]$ corresponds to ``in phase'' vibration of the two string endpoints, i.e., $ F_v(e^{j\omega T}) = F_h(e^{j\omega T})$, while $ \underline{e}_T=[1, -1]$ corresponds to ``opposite phase'' vibration, for which $ F_v(e^{j\omega T}) = -F_h(e^{j\omega T})$. If it happens to be the case that

$\displaystyle \vert A+B\vert<\vert A-B\vert $

then the in-phase vibration component will decay faster than the opposite-phase vibration. This situation applies to coupled piano strings [543], as discussed further below.

More generally, the two eigenvectors of the coupling frequency-response matrix

$\displaystyle \mathbf{H}(e^{j\omega}) \isdef \left[\begin{array}{cc} H_{vv}(e^{... ...\omega}) \\ [2pt] H_{hv}(e^{j\omega}) & H_{hh}(e^{j\omega}) \end{array}\right] $

correspond to two decoupled polarization planes. That is, at each frequency there are two eigenpolarizations in which incident vibration reflects in the same plane. In general, the eigenplanes change with frequency. A related analysis is given in [543].

By definition of the eigenvectors of $ \mathbf{H}(e^{j\omega T})$, we have

$\displaystyle \mathbf{H}(e^{j\omega T}) \underline{e}_i(e^{j\omega T}) = \lambda_i(e^{j\omega T})\underline{e}_i(e^{j\omega T}) $

where $ \lambda_i(e^{j\omega T})$ denotes the $ i$th eigenvalue of the coupling-matrix $ \mathbf{H}(e^{j\omega T})$ at frequency $ \omega $, where $ i=1,2$. Since the eigenvector $ \underline{e}_i(e^{j\omega T})$ holds the Fourier transform of the incoming waves for mode $ i$ of the coupled-string system, we see that the eigenvalues have the following interpretation:
The $ i$th eigenvalue of the coupling matrix equals the frequency response seen by the $ i$th eigenpolarization.
In particular, the modulus of the eigenvalue gives the reflectance magnitude (affecting mode damping), and the angle of the eigenvalue is the phase shift of the reflection, for that mode (affecting tuning of the mode). Use of coupling matrix eigenanalysis to determine mode damping and tuning is explored further in §C.13.

Next Section:
Asymmetry of Horizontal/Vertical Terminations
Previous Section:
Horizontal and Vertical Transverse Waves