The Ideal Plucked String
The ideal plucked string is defined as an initial string
displacement and a zero initial velocity distribution [317]. More
generally, the initial displacement along the string ![]() and the
initial velocity distribution
and the
initial velocity distribution
![]() , for all
, for all ![]() , fully determine the
resulting motion in the absence of further excitation.
, fully determine the
resulting motion in the absence of further excitation.
An example of the appearance of the traveling-wave components and the resulting string shape shortly after plucking a doubly terminated string at a point one fourth along its length is shown in Fig.6.7. The negative traveling-wave portions can be thought of as inverted reflections of the incident waves, or as doubly flipped ``images'' which are coming from the other side of the terminations.
An example of an initial ``pluck'' excitation in a digital waveguide string model is shown in Fig.6.8. The circulating triangular components in Fig.6.8 are equivalent to the infinite train of initial images coming in from the left and right in Fig.6.7.
There is one fine-point to note for the discrete-time case:
We cannot admit a sharp corner
in the string since that would have infinite bandwidth which would alias
when sampled. Therefore, for the discrete-time case, we define the ideal
pluck to consist of an arbitrary shape as in
Fig.6.8 lowpass filtered to less than half
the sampling rate. Alternatively, we can simply require the initial
displacement shape to be bandlimited to spatial frequencies less than
![]() . Since all real strings have some degree of stiffness which
prevents the formation of perfectly sharp corners, and since real plectra
are never in contact with the string at only one point, and since the
frequencies we do allow span the full range of human hearing, the
bandlimited restriction is not limiting in any practical sense.
. Since all real strings have some degree of stiffness which
prevents the formation of perfectly sharp corners, and since real plectra
are never in contact with the string at only one point, and since the
frequencies we do allow span the full range of human hearing, the
bandlimited restriction is not limiting in any practical sense.
![\includegraphics[width=\twidth]{eps/fidealpluck}](http://www.dsprelated.com/josimages_new/pasp/img1395.png) |
Note that acceleration (or curvature) waves are a simple choice for
plucked string simulation, since the ideal pluck corresponds to an initial
impulse in the delay lines at the pluck point. Of course, since we
require a bandlimited excitation, the initial acceleration distribution
will be replaced by the impulse response of the anti-aliasing filter
chosen.
If the anti-aliasing filter chosen is the ideal lowpass filter cutting off
at ![]() , the initial acceleration
, the initial acceleration
![]() for the
ideal pluck becomes
for the
ideal pluck becomes
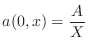 sinc sinc |
(7.13) |
where
Aside from its obvious simplicity, there are two important benefits of obtaining an impulse-excited model: (1) an extremely efficient ``commuted synthesis'' algorithm can be readily defined (§8.7), and (2) linear prediction (and its relatives) can be readily used to calibrate the model to recordings of normally played tones on the modeled instrument. Linear Predictive Coding (LPC) has been used extensively in speech modeling [296,297,20]. LPC estimates the model filter coefficients under the assumption that the driving signal is spectrally flat. This assumption is valid when the input signal is (1) an impulse, or (2) white noise. In the basic LPC model for voiced speech, a periodic impulse train excites the model filter (which functions as the vocal tract), and for unvoiced speech, white noise is used as input.
In addition to plucked and struck strings, simplified bowed strings can be calibrated to recorded data as well using LPC [428,439]. In this simplified model, the bowed string is approximated as a periodically plucked string.
![\includegraphics[width=\twidth]{eps/fpluckaccel}](http://www.dsprelated.com/josimages_new/pasp/img1405.png) |
Next Section:
The Ideal Struck String
Previous Section:
Moving Rigid Termination








![\includegraphics[width=\twidth]{eps/f_t_waves_term}](http://www.dsprelated.com/josimages_new/pasp/img1393.png)











