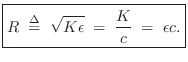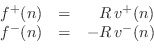DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Ideal Vibrating String

Figure 6.1: The ideal vibrating string.
\includegraphics[scale=0.9]{eps/FphysicalstringCopy}

The ideal vibrating string is depicted in Fig.6.1. It is assumed to be perfectly flexible and elastic. Once ``plucked,'' it will vibrate forever in one plane as an energy conserving system. The mathematical theory of string vibration is considered in §B.6 and Appendix C. For present purposes, we only need some basic definitions and results.

Wave Equation

The wave equation for the ideal vibrating string may be written as

$\displaystyle Ky''= \epsilon {\ddot y}$ (7.1)

where we define the following notation:

\begin{displaymath}\begin{array}{rclrcl} K& \isdef & \mbox{string tension} & \qq... ...isdef & \frac{\partial}{\partial x}y(t,x) \nonumber \end{array}\end{displaymath}    

As discussed in Chapter 1, the wave equation in this form can be interpreted as a statement of Newton's second law,

$\displaystyle \textit{force} = \textit{mass} \times \textit{acceleration}, $

on a microscopic scale. Since we are concerned with transverse vibrations on the string, the relevant restoring force (per unit length) is given by the string tension (force along the string axis) times the curvature of the string, or $ Ky''(t,x)$; the restoring force is balanced at all times by the inertial force per unit length of the string which is equal to mass density (mass per unit length) times transverse acceleration, i.e., $ \epsilon {\ddot y}(t,x)$. See Appendix B for a review of basic physical concepts. The wave equation is derived in some detail in §B.6.

Wave Equation Applications

The ideal-string wave equation applies to any perfectly elastic medium which is displaced along one dimension. For example, the air column of a clarinet or organ pipe can be modeled using the one-dimensional wave equation by substituting air-pressure deviation for string displacement, and longitudinal volume velocity for transverse string velocity. We refer to the general class of such media as one-dimensional waveguides. Extensions to two and three dimensions (and more, for the mathematically curious), are also possible (see §C.14) [518,520,55].

For a physical string model, at least three coupled waveguide models should be considered. Two correspond to transverse-wave vibrations in the horizontal and vertical planes (two polarizations of planar vibration); the third corresponds to longitudinal waves. For bowed strings, torsional waves should also be considered, since they affect bow-string dynamics [308,421]. In the piano, for key ranges in which the hammer strikes three strings simultaneously, nine coupled waveguides are required per key for a complete simulation (not including torsional waves); however, in a practical, high-quality, virtual piano, one waveguide per coupled string (modeling only the vertical, transverse plane) suffices quite well [42,43]. It is difficult to get by with fewer than the correct number of strings, however, because their detuning determines the entire amplitude envelope as well as beating and aftersound effects [543].

Traveling-Wave Solution

It can be readily checked (see §C.3 for details) that the lossless 1D wave equation

$\displaystyle Ky''= \epsilon {\ddot y}$

(where all terms are defined in Eq.$ \,$(6.1)) is solved by any string shape which travels to the left or right with speed

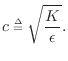
$\displaystyle c \isdeftext \sqrt{\frac{K}{\epsilon }}. $

If we denote right-going traveling waves in general by $ y_r(t-x/c)$ and left-going traveling waves by $ y_l(t+x/c)$, where $ y_r$ and $ y_l$ are arbitrary twice-differentiable functions, then the general class of solutions to the lossless, one-dimensional, second-order wave equation can be expressed as

$\displaystyle y(t,x) = y_r(t-x/c) + y_l(t+x/c). \protect$ (7.2)

Note that we have $ {\ddot y}_r= c^2y''_r$ and $ {\ddot y}_l= c^2y''_l$ (derived in §C.3.1) showing that the wave equation is satisfied for all traveling wave shapes $ y_r$ and $ y_l$. However, the derivation of the wave equation itself assumes the string slope $ \vert y^\prime\vert$ is much less than $ 1$ at all times and positions (see §B.6). An important point to note is that a function of two variables $ y(t,x)$ is replaced by two functions of a single (time) variable. This leads to great reductions in computational complexity, as we will see. The traveling-wave solution of the wave equation was first published by d'Alembert in 1747 [100]7.1

Sampled Traveling-Wave Solution

As discussed in more detail in Appendix C, the continuous traveling-wave solution to the wave equation given in Eq.$ \,$(6.2) can be sampled to yield

$\displaystyle y(nT,mX)$ $\displaystyle =$ $\displaystyle y_r(nT-mX/c) + y_l(nT+mX/c)$   $\displaystyle \mbox{(set $X=cT$)}$  
  $\displaystyle =$ $\displaystyle y_r(nT-mT) + y_l(nT+mT)$  
  $\displaystyle \isdef$ $\displaystyle y^{+}(n-m) + y^{-}(n+m) \protect,$ (7.3)

where $ T$ denotes the time sampling interval in seconds, $ X=cT$ denotes the spatial sampling interval in meters, and $ y^{+}$ and $ y^{-}$ are defined for notational convenience.

Wave Impedance

A concept of high practical utility is that of wave impedance, defined for vibrating strings as force divided by velocity. As derived in §C.7.2, the relevant force quantity in this case is minus the string tension times the string slope:

$\displaystyle f(t,x) \isdef -Ky'(t,x)$ (7.4)

Physically, this can be regarded as the transverse force acting to the right on the string in the vertical direction. (Only transverse vibration is being considered.) In other words, the vertical component of a negative string slope pulls ``up'' on the segment of string to the right, and ``up'' is the positive direction for displacement, velocity, and now force. The traveling-wave decomposition of the force into force waves is thus given by (see §C.7.2 for a more detailed derivation)7.2

\begin{eqnarray*} f(t,x) &=& f_r(t-x/c) + f_l(t+x/c)\\ &=& -Ky'_r(t-x/c) - Ky'... ...}{c}{\dot y}_l(t+x/c)\\ &\isdef & R{v_r}(t-x/c) - Rv_l(t+x/c), \end{eqnarray*}

where we have defined the new notation $ v={\dot y}$ for transverse velocity, and

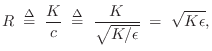
$\displaystyle R\isdefs \frac{K}{c} \isdefs \frac{K}{\sqrt{K/\epsilon }} \eqsp \sqrt{K\epsilon }, $

where $ K$ is the string tension and $ \epsilon $ is mass density. The newly defined positive constant $ R=\sqrt{K\epsilon }$ is called the wave impedance of the string for transverse waves. It is always real and positive for the ideal string. Three expressions for the wave impedance are

$\displaystyle \zbox {R\isdefs \sqrt{K\epsilon } \eqsp \frac{K}{c} \eqsp \epsilon c.} \protect$ (7.5)

The wave impedance simply relates force and velocity traveling waves:

\begin{displaymath}\begin{array}{rcr@{\,}l} f^{{+}}(n)&=&&\!R\,v^{+}(n) \\ f^{{-... ...\end{array} \protect% FIXHTML: Causes a strange button in HTML \end{displaymath} (7.6)

These relations may be called Ohm's law for traveling waves. Thus, in a traveling wave, force is always in phase with velocity (considering the minus sign in the left-going case to be associated with the direction of travel rather than a $ 180$ degrees phase shift between force and velocity).

The results of this section are derived in more detail in Appendix C. However, all we need in practice for now are the important Ohm's law relations for traveling-wave components given in Eq.$ \,$(6.6).

Next Section:
Ideal Acoustic Tube
Previous Section:
The Leslie