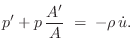Momentum Conservation in Nonuniform Tubes
Newton's second law ``force equals mass times acceleration'' implies that
the pressure gradient in a gas is proportional to the acceleration of a
differential volume element in the gas. Let ![]() denote the area of the
surface of constant phase at radial coordinate
denote the area of the
surface of constant phase at radial coordinate ![]() in the tube. Then the
total force acting on the surface due to pressure is
in the tube. Then the
total force acting on the surface due to pressure is
![]() , as
shown in Fig.C.45.
, as
shown in Fig.C.45.
The net force ![]() to the right across the volume element
between
to the right across the volume element
between ![]() and
and ![]() is then
is then
where, when time and/or position arguments have been dropped, as in the last line above, they are all understood to be
![\begin{eqnarray*}
dM(t,x) &=& \int_x^{x+dx} \rho(t,\xi) A(\xi)\,d\xi \\ [5pt]
&\...
...\rho A' \right)\frac{(dx)^2}{2}\\ [5pt]
&\approx& \rho\, A\,dx,
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img4273.png)
where ![]() denotes air density.
denotes air density.
The center-of-mass acceleration of the volume element can be written
as
![]() where
where ![]() is particle velocity.C.16 Applying Newton's second law
is particle velocity.C.16 Applying Newton's second law
![]() , we
obtain
, we
obtain
or, dividing through by
In terms of the logarithmic derivative of
Note that
Cylindrical Tubes
In the case of cylindrical tubes, the logarithmic derivative of the
area variation,
ln![]() , is zero, and Eq.
, is zero, and Eq.![]() (C.148)
reduces to the usual momentum conservation equation
(C.148)
reduces to the usual momentum conservation equation
![]() encountered when deriving the wave equation for plane waves
[318,349,47]. The present case reduces to the
cylindrical case when
encountered when deriving the wave equation for plane waves
[318,349,47]. The present case reduces to the
cylindrical case when
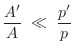
If we look at sinusoidal spatial waves,
![]() and
and
![]() , then
, then
![]() and
and
![]() , and the condition
for cylindrical-wave behavior becomes
, and the condition
for cylindrical-wave behavior becomes
![]() , i.e., the spatial
frequency of the wall variation must be much less than that of the
wave. Another way to say this is that the wall must be approximately
flat across a wavelength. This is true for smooth horns/bores at
sufficiently high wave frequencies.
, i.e., the spatial
frequency of the wall variation must be much less than that of the
wave. Another way to say this is that the wall must be approximately
flat across a wavelength. This is true for smooth horns/bores at
sufficiently high wave frequencies.
Next Section:
Wave Impedance in a Cone
Previous Section:
Conical Acoustic Tubes








![\includegraphics[width=3in]{eps/fconic}](http://www.dsprelated.com/josimages_new/pasp/img4265.png)