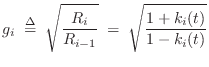Normalized Scattering Junctions

Free Books Physical Audio Signal Processing

**Figure C.22:** The normalized scattering junction.
$\includegraphics[scale=0.9]{eps/scatnlf}$

Using (C.53) to convert to normalized waves $\tilde{f}^\pm$ , the Kelly-Lochbaum junction (C.60) becomes

$\displaystyle \tilde{f}^{+}_i(t)$	$\displaystyle =$	$\displaystyle \sqrt{1-k_i^2(t)}\, \tilde{f}^{+}_{i-1}(t-T) - k_i(t)\, \tilde{f}^{-}_i(t)$
$\displaystyle \tilde{f}^{-}_{i-1}(t+T)$	$\displaystyle =$	$\displaystyle k_i(t)\,\tilde{f}^{+}_{i-1}(t-T) + \sqrt{1-k_i^2(t)}\,\tilde{f}^{-}_i(t)$	(C.66)

as diagrammed in Fig.C.22. This is called the normalized scattering junction [297], although a more precise term would be the ``normalized-wave scattering junction.''

It is interesting to define $\theta_i \isdef \sin^{-1}(k_i)$ , always possible for passive junctions since $-1\leq k_i\leq 1$ , and note that the normalized scattering junction is equivalent to a 2D rotation:

$\displaystyle \tilde{f}^{+}_i(t)$	$\displaystyle =$	$\displaystyle \cos(\theta_i) \, \tilde{f}^{+}_{i-1}(t-T) - \sin(\theta_i) \, \tilde{f}^{-}_i(t)$
$\displaystyle \tilde{f}^{-}_{i-1}(t+T)$	$\displaystyle =$	$\displaystyle \sin(\theta_i)\, \tilde{f}^{+}_{i-1}(t-T) + \cos(\theta_i)\, \tilde{f}^{-}_i(t)$	(C.67)

where, for conciseness of notation, the time-invariant case is written.

While it appears that scattering of normalized waves at a two-port junction requires four multiplies and two additions, it is possible to convert this to three multiplies and three additions using a two-multiply ``transformer'' to power-normalize an ordinary one-multiply junction [432].

The transformer is a lossless two-port defined by [136]

$\displaystyle f^{{+}}_i(t)$	$\displaystyle =$	$\displaystyle g_i\, f^{{+}}_{i-1}(t-T)$
$\displaystyle f^{{-}}_{i-1}(t+T)$	$\displaystyle =$	$\displaystyle \frac{1}{g_i}\,f^{{-}}_i(t).$	(C.68)

The transformer can be thought of as a device which steps the wave impedance to a new value without scattering; instead, the traveling signal power is redistributed among the force and velocity wave variables to satisfy the fundamental relations $f^\pm =\pm Rv^\pm$ (C.57) at the new impedance. An impedance change from $R_{i-1}$ on the left to

on the right is accomplished using

$\displaystyle g_i \isdefs \sqrt\frac{R_i}{R_{i-1}} \eqsp \sqrt\frac{1+k_i(t)}{1-k_i(t)} \protect$

(C.69)

as can be quickly derived by requiring $(f^{{+}}_{i-1})^2/R_{i-1}= (f^{{+}}_i)^2/R_i$ . The parameter

can be interpreted as the ``turns ratio'' since it is the factor by which force is stepped (and the inverse of the velocity step factor).

**Figure C.23:** Three-multiply normalized-wave scattering junction.
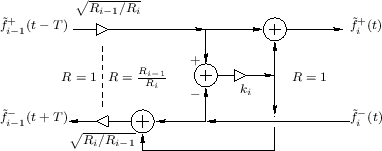
$\includegraphics{eps/scatThreeMulNLFx}$

Figure C.23 illustrates a three-multiply normalized-wave scattering junction [432]. The impedance of all waveguides (bidirectional delay lines) may be taken to be . Scattering junctions may then be implemented as a denormalizing transformer $g=\sqrt{R_{i-1}}$ , a one-multiply scattering junction , and a renormalizing transformer $g=1/\sqrt{R_i}$ . Either transformer may be commuted with the junction and combined with the other transformer to give a three-multiply normalized-wave scattering junction. (The transformers are combined on the left in Fig.C.23).

In slightly more detail, a transformer $g=\sqrt{R_{i-1}}$ steps the wave impedance (left-to-right) from to $R=R_{i-1}$ . Equivalently, the normalized force-wave $\tilde{f}^{+}_{i-1}(t)$ is converted unnormalized form $f^{{+}}_{i-1}(t)$ . Next there is a physical scattering from impedance $R_{i-1}$ to (reflection coefficient $k_i=(R_i-R_{i-1})/(R_i+R_{i-1})$ ). The outgoing wave to the right is then normalized by transformer $g=1/\sqrt{R_i}$ to return the wave impedance back to for wave propagation within a normalized-wave delay line to the right. Finally, the right transformer is commuted left and combined with the left transformer to reduce total computational complexity to one multiply and three adds.

It is important to notice that transformer-normalized junctions may have a large dynamic range in practice. For example, if $k_i\in [-1+\epsilon,1-\epsilon]$ , then Eq. $\,$ (C.69) shows that the transformer coefficients may become as large as $\sqrt{2/\epsilon - 1}$ . If $\epsilon$ is the ``machine epsilon,'' i.e., $\epsilon = 2^{-(n-1)}$ for typical -bit two's complement arithmetic normalized to lie in , then the dynamic range of the transformer coefficients is bounded by $\sqrt{2^n-1}\approx 2^{n/2}$ . Thus, while transformer-normalized junctions trade a multiply for an add, they require up to % more bits of dynamic range within the junction adders. On the other hand, it is very nice to have normalized waves (unit wave impedance) throughout the digital waveguide network, thereby limiting the required dynamic range to root physical power in all propagation paths.