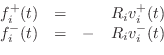Longitudinal Waves in Rods
In this section, elementary scattering relations will be derived for the case of longitudinal force and velocity waves in an ideal string or rod. In solids, force-density waves are referred to as stress waves [169,261]. Longitudinal stress waves in strings and rods have units of (compressive) force per unit area and are analogous to longitudinal pressure waves in acoustic tubes.
![\includegraphics[width=\twidth]{eps/Fwgfs}](http://www.dsprelated.com/josimages_new/pasp/img3577.png) |
A single waveguide section between two partial sections is shown in
Fig.C.19. The sections are numbered 0 through ![]() from
left to right, and their wave impedances are
from
left to right, and their wave impedances are ![]() ,
, ![]() , and
, and ![]() ,
respectively. Such a rod might be constructed, for example, using
three different materials having three different densities. In the
,
respectively. Such a rod might be constructed, for example, using
three different materials having three different densities. In the
![]() th section, there are two stress traveling waves:
th section, there are two stress traveling waves: ![]() traveling
to the right at speed
traveling
to the right at speed ![]() , and
, and ![]() traveling to the left at speed
traveling to the left at speed
![]() . To minimize the numerical dynamic range, velocity waves may be
chosen instead when
. To minimize the numerical dynamic range, velocity waves may be
chosen instead when ![]() .
.
As in the case of transverse waves (see the derivation of (C.46)), the traveling longitudinal plane waves in each section satisfy [169,261]
where the wave impedance is now
If the wave impedance ![]() is constant, the shape of a traveling wave
is not altered as it propagates from one end of a rod-section to the
other. In this case we need only consider
is constant, the shape of a traveling wave
is not altered as it propagates from one end of a rod-section to the
other. In this case we need only consider ![]() and
and ![]() at one
end of each section as a function of time. As shown in Fig.C.19,
we define
at one
end of each section as a function of time. As shown in Fig.C.19,
we define
![]() as the force-wave component at the extreme
left of section
as the force-wave component at the extreme
left of section ![]() . Therefore, at the extreme right of section
. Therefore, at the extreme right of section ![]() ,
we have the traveling waves
,
we have the traveling waves
![]() and
and
![]() , where
, where ![]() is
the travel time from one end of a section to the other.
is
the travel time from one end of a section to the other.
For generality, we may allow the wave impedances ![]() to vary with
time. A number of possibilities exist which satisfy (C.57) in the
time-varying case. For the moment, we will assume the traveling waves
at the extreme right of section
to vary with
time. A number of possibilities exist which satisfy (C.57) in the
time-varying case. For the moment, we will assume the traveling waves
at the extreme right of section ![]() are still given by
are still given by
![]() and
and
![]() . This definition, however, implies the velocity varies
inversely with the wave impedance. As a result, signal energy, being the product
of force times velocity, is ``pumped'' into or out of the waveguide
by a changing wave impedance. Use of normalized waves
. This definition, however, implies the velocity varies
inversely with the wave impedance. As a result, signal energy, being the product
of force times velocity, is ``pumped'' into or out of the waveguide
by a changing wave impedance. Use of normalized waves
![]() avoids this.
However, normalization increases the required number of
multiplications, as we will see in §C.8.6 below.
avoids this.
However, normalization increases the required number of
multiplications, as we will see in §C.8.6 below.
As before, the physical force density (stress) and velocity at the
left end of section ![]() are obtained by summing the left- and
right-going traveling wave components:
are obtained by summing the left- and
right-going traveling wave components:
Let
Next Section:
Kelly-Lochbaum Scattering Junctions
Previous Section:
Plane-Wave Scattering at an Angle