DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Passive String Terminations

When a traveling wave reflects from the bridge of a real stringed instrument, the bridge moves, transmitting sound energy into the instrument body. How far the bridge moves is determined by the driving-point impedance of the bridge, denoted $ R_b(s)$. The driving point impedance is the ratio of Laplace transform of the force on the bridge $ F_b(s)$ to the velocity of motion that results $ V_b(s)$. That is, $ R_b(s)\isdeftext F_b(s)/V_b(s)$.

For passive systems (i.e., for all unamplified acoustic musical instruments), the driving-point impedance $ R_b(s)$ is positive real (a property defined and discussed in §C.11.2). Being positive real has strong implications on the nature of $ R_b(s)$. In particular, the phase of $ R_b(j\omega)$ cannot exceed plus or minus $ 90$ degrees at any frequency, and in the lossless case, all poles and zeros must interlace along the $ j\omega $ axis. Another implication is that the reflectance of a passive bridge, as seen by traveling waves on the string, is a so-called Schur function (defined and discussed in §C.11); a Schur reflectance is a stable filter having gain not exceeding 1 at any frequency. In summary, a guitar bridge is passive if and only if its driving-point impedance is positive real and (equivalently) its reflectance is Schur. See §C.11 for a fuller discussion of this point.

At $ x=0$, the force on the bridge is given by (§C.7.2)

$\displaystyle f_b(t) \eqsp Ky'(t,0) \eqsp - f(t,0) $

where $ K$ is the string tension as in Chapter 6, and $ y'(t,0)$ is the slope of the string at $ x=0$. In the Laplace frequency domain, we have

$\displaystyle F_b(s) \eqsp KY'(s,0) \eqsp - F(s,0), $

due to linearity, and the velocity of the string endpoint is therefore

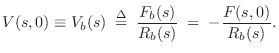
$\displaystyle V(s,0) \equiv V_b(s) \isdefs \frac{F_b(s)}{R_b(s)} \eqsp -\frac{F(s,0)}{R_b(s)}. $

Next Section:
A Terminating Resonator
Previous Section:
Software for Cubic Nonlinear Distortion