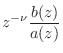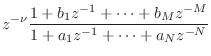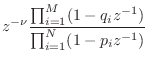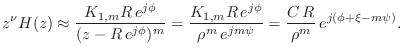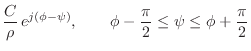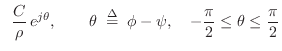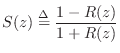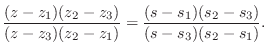Positive Real Functions

Free Books Physical Audio Signal Processing

Any passive driving-point impedance, such as the impedance of a violin bridge, is positive real. Positive real functions have been studied extensively in the continuous-time case in the context of network synthesis [68,524]. Very little, however, seems to be available in the discrete time case. This section (reprinted from [428]) summarizes the main properties of positive real function in the plane (i.e., the discrete-time case).

Definition. A complex valued function of a complex variable is said to be positive real (PR) if

$z\ real\,\implies f(z)\ real$
$\left\vert z\right\vert\geq 1\implies$ re $\left\{f(z)\right\}\geq 0$

We now specialize to the subset of functions representable as a ratio of finite-order polynomials in . This class of ``rational'' functions is the set of all transfer functions of finite-order time-invariant linear systems, and we write to denote a member of this class. We use the convention that stable, minimum phase systems are analytic and nonzero in the strict outer disk.^C.8 Condition (1) implies that for to be PR, the polynomial coefficients must be real, and therefore complex poles and zeros must exist in conjugate pairs. We assume from this point on that $H(z)\neq 0$ satisfies (1). From (2) we derive the facts below.

Property 1. A real rational function is PR iff $\left\vert z\right\vert\geq 1 \implies \left\vert\angle{H(z)}\right\vert\leq \frac{\pi}{2}$ .

Proof. Expressing in polar form gives

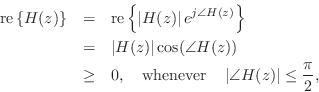
$\begin{eqnarray*} \mbox{re}\left\{H(z)\right\} &=& \mbox{re}\left\{\left\vert H... ...er} \quad \left\vert\angle{H(z)}\right\vert\leq \frac{\pi}{2}, \end{eqnarray*}$

since the zeros of are isolated. $\Box$

Property 2. is PR iff is PR.

Proof. Assuming is PR, we have by Property 1,

$\displaystyle \left\vert\angle{H^{-1}(z)}\right\vert = \left\vert-\angle{H(z)}\... ...angle{H(z)}\right\vert \leq \frac{\pi}{2},\quad \left\vert z\right\vert\geq 1.$

$\Box$

Property 3. A PR function is analytic and nonzero in the strict outer disk.

Proof. (By contradiction)

Without loss of generality, we treat only $n^{th}$ order polynomials

$\displaystyle \alpha_0z^n + \alpha_1z^{n-1} + \cdots + \alpha_{n-1}z + \alpha_n$

which are nondegenerate in the sense that $\alpha_0,\alpha_n\neq 0$ . Since facts about $\alpha_0 H(z)$ are readily deduced from facts about

, we set $\alpha_0 = 1$ at no great loss.

The general (normalized) causal, finite-order, linear, time-invariant transfer function may be written

$\displaystyle H(z)$	$\displaystyle =$	$\displaystyle z^{-\nu}\frac{b(z)}{a(z)}$
	$\displaystyle =$	$\displaystyle z^{-\nu}\frac{1 + b_1 z^{-1} + \cdots + b_M z^{-M} }{ 1 + a_1 z^{-1} + \cdots + a_N z^{-N} }$
	$\displaystyle =$	$\displaystyle z^{-\nu}\frac{ \prod_{i=1}^M (1 - q_i z^{-1}) }{ \prod_{i=1}^N (1 - p_i z^{-1}) }$
	$\displaystyle =$	$\displaystyle z^{-\nu}\sum_{i=1}^{N_d} \sum_{j=1}^{\mu_i} \frac{z\,K_{i,j} }{ (z-p_i)^j} , \qquad \nu\geq 0,$	(C.80)

where

is the number of distinct poles, each of multiplicity $\mu_i$ ,and

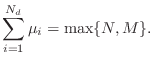
$\displaystyle \sum_{i=1}^{N_d}\mu_i = \max\{N,M\}.$

Suppose there is a pole of multiplicity outside the unit circle. Without loss of generality, we may set $\mu_1=m$ , and $p_1 = R\,e^{j\phi}$ with . Then for near , we have

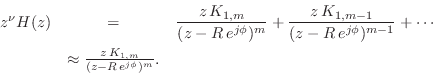
$\begin{eqnarray*} z^\nu H(z) &=&\frac{ z\,K_{1,m} }{ (z-R\,e^{j\phi})^m} + \fr... ...+ \cdots\\ & \approx \frac{z\, K_{1,m} }{ (z-R\,e^{j\phi})^m}. \end{eqnarray*}$

Consider the circular neighborhood of radius $\rho$ described by $z=R\,e^{j\phi}+ \rho\,e^{j\psi},\;-\pi\leq \psi<\pi$ . Since we may choose $\rho < R-1$ so that all points in this neighborhood lie outside the unit circle. If we write the residue of the factor $(z-R\,e^{j\phi})^m$ in polar form as $K_{1,m}=C\,e^{j\xi}$ , then we have, for sufficiently small $\rho$ ,

$\displaystyle z^\nu H(z) \approx \frac{K_{1,m}R\,e^{j\phi}}{ (z-R\,e^{j\phi})^m... ...\phi}}{ \rho^m\,e^{jm\psi}} = \frac{C\,R}{ \rho^m}\, e^{j(\phi + \xi - m\psi)}.$

(C.81)

Therefore, approaching the pole $R\,e^{j\phi}$ at an angle $\psi$ gives

$\displaystyle \lim_{\rho\to 0}\left\vert\angle{H(R\,e^{j\phi}+\rho\,e^{j\psi})}... ... = \left\vert\phi(1-\nu) + \xi - m\psi \right\vert, \qquad -\pi \leq \psi <\pi$

which cannot be confined to satisfy Property 1 regardless of the value of the residue angle $\xi$ , or the pole angle $\phi$ (

cannot be zero by hypothesis). We thus conclude that a PR function

can have no poles in the outer disk. By Property 2, we conclude that positive real functions must be minimum phase. $\Box$

Corollary. In equation Eq. $\,$ (C.80), $\nu=0$ .

Proof. If $\nu>0$ , then there are $\nu$ poles at infinity. As $\left\vert z\right\vert\to \infty$ , $H(z)\to z^{-\nu} \implies \left\vert\angle{H(z)}\right\vert \to \left\vert\nu\angle{z}\right\vert$ , we must have $\nu=0$ . $\Box$

Corollary. The log-magnitude of a PR function has zero mean on the unit circle.

This is a general property of stable, minimum-phase transfer functions which follows immediately from the argument principle [297,326].

Corollary. A rational PR function has an equal number of poles and zeros all of which are in the unit disk.

This really a convention for numbering poles and zeros. In Eq. $\,$ (C.80), we have $\nu=0$ , and all poles and zeros inside the unit disk. Now, if then we have extra poles at induced by the numerator. If , then zeros at the origin appear from the denominator.

Corollary. Every pole on the unit circle of a positive real function must be simple with a real and positive residue.

Proof. We repeat the previous argument using a semicircular neighborhood of radius $\rho$ about the point $p_1 = e^{j\phi}$ to obtain

$\displaystyle \lim_{\rho\to 0}\left\vert\angle{H(e^{j\phi} + \rho e^{j\psi})}\r... ...m\psi \right\vert,\qquad \phi-\frac{\pi}{2} \leq \psi\leq \phi + \frac{\pi}{2}.$

(C.82)

In order to have $\left\vert\angle{H(z)}\right\vert\leq \pi/2$ near this pole, it is necessary that

and $\xi=0$ . $\Box$

Corollary. If is PR with a zero at $z=q_1=e^{j\phi}$ , then

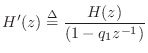
$\displaystyle H^\prime(z) \isdef \frac{H(z)}{ (1-q_1 z^{-1})}$

must satisfy

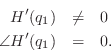
$\begin{eqnarray*} H^\prime(q_1) &\neq& 0 \\ \angle{H^\prime(q_1)}&=& 0 . \end{eqnarray*}$

Proof. We may repeat the above for .

Property. Every PR function has a causal inverse z transform .

Proof. This follows immediately from analyticity in the outer disk [342, pp. 30-36] However, we may give a more concrete proof as follows. Suppose is non-causal. Then there exists such that $h(-k)\neq 0$ . We have,

$\begin{eqnarray*} H(z)\;&\isdef & \sum_{n=-\infty }^\infty h(n)\,z^{-n}\\ &=& h(-k)z^k + \sum_{n \neq -k} h(n)\,z^{-n}. \end{eqnarray*}$

Hence, has at least one pole at infinity and cannot be PR by Property 3. Note that this pole at infinity cannot be cancelled since otherwise

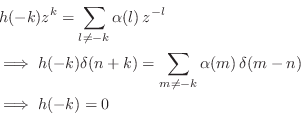
$\begin{eqnarray*} && h(-k)z^k = \sum_{l\neq -k}\alpha(l)\,z^{-l}\\ &&\implies... ... \sum_{m\neq -k}\alpha(m)\,\delta(m-n)\\ &&\implies h(-k) = 0 \end{eqnarray*}$

which contradicts the hypothesis that is non-causal. $\Box$

Property. is PR iff it is analytic for $\left\vert z\right\vert>1$ , poles on the unit circle are simple with real and positive residues, and re $\left\{\\ right\}{H(e^{j\theta})\}\geq 0$ for $0\leq \theta\leq \pi$ .

Proof. If is positive real, the conditions stated hold by virtue of Property 3 and the definition of positive real.

To prove the converse, we first show nonnegativity on the upper semicircle implies nonnegativity over the entire circle.

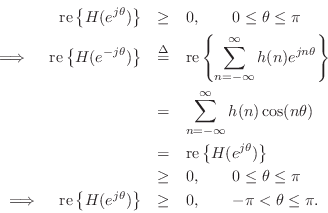
$\begin{eqnarray*} \mbox{re}\left\{H(e^{j\theta})\right\} &\geq& 0, \qquad 0 \leq... ...eft\{H(e^{j\theta})\right\}&\geq& 0, \qquad -\pi<\theta\leq \pi. \end{eqnarray*}$

Alternatively, we might simply state that real implies re $\left\{H(e^{j\theta})\right\}$ is even in $\theta$ .

Next, since the function is analytic everywhere except at $z=\infty$ , it follows that $f(z)=e^{-H(z)}$ is analytic wherever is finite. There are no poles of outside the unit circle due to the analyticity assumption, and poles on the unit circle have real and positive residues. Referring again to the limiting form Eq. $\,$ (C.81) of near a pole on the unit circle at $e^{j\phi}$ , we see that, as ${\rho \to 0}$ , we have

$\displaystyle H(e^{j\phi} + \rho\,e^{j\psi})$	$\displaystyle \to$	$\displaystyle \frac{C}{ \rho}\, e^{j(\phi - \psi)}, \qquad \phi- \frac{\pi}{2} \leq \psi\leq \phi + \frac{\pi}{2}$
	$\displaystyle \isdef$	$\displaystyle \;\; \frac{C}{ \rho}\,e^{j\theta}, \qquad \theta \isdefs \phi - \psi, \quad - \frac{\pi}{ 2} \leq \theta \leq \frac{\pi}{ 2}$
$\displaystyle \implies \quad f(z)$	$\displaystyle \to$	$\displaystyle e^{- \frac{C}{ \rho}\, e^{j\theta}}$
	$\displaystyle =$	$\displaystyle e^{- \frac{C}{ \rho}\, \cos\theta} e^{-j \frac{C}{ \rho}\,\sin\theta}$
	$\displaystyle \to$	$\displaystyle 0, \protect$	(C.83)

since the residue

is positive, and the net angle $\theta$ does not exceed $\pm\pi/2$ . From Eq. $\,$ (C.83) we can state that for points $z,z^\prime$ with modulus $\geq 1$ , we have For all $\epsilon>0$ , there exists $\delta>0$ such that $\left\vert z-z^\prime \right\vert<\delta \;\implies\; \left\vert f(z)-f(z^\prime )\right\vert<\epsilon$ . Thus

is analytic in the strict outer disk, and continuous up to the unit circle which forms its boundary. By the maximum modulus theorem [83],

$\displaystyle \sup_{\left\vert z\right\vert\geq 1} \left\vert f(z)\right\vert \... ...)\right\}} = \inf_{\left\vert z\right\vert\geq 1} \mbox{re}\left\{H(z)\right\}$

occurs on the unit circle. Consequently,

$\displaystyle \inf_{-\pi<\theta\leq \pi}$ re $\displaystyle \left\{H(e^{j\theta})\right\}\geq 0 \quad\implies\quad\inf_{\left\vert z\right\vert\geq 1}$ re $\displaystyle \left\{H(z)\right\}\geq 0 \quad\implies\quad H(z)\;PR\,.$

For example, if a transfer function is known to be asymptotically stable, then a frequency response with nonnegative real part implies that the transfer function is positive real.

Note that consideration of leads to analogous necessary and sufficient conditions for to be positive real in terms of its zeros instead of poles. $\Box$

Relation to Stochastic Processes

Property. If a stationary random process $\{x_n\}$ has a rational power spectral density $Re^{j\omega}$ corresponding to an autocorrelation function $r(k)={\cal E}\left\{x_nx_{n+k}\right\}$ , then

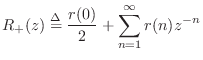
$\displaystyle R_+(z)\isdef \frac{r(0)}{ 2} + \sum_{n=1}^\infty r(n)z^{-n}$

is positive real.

Proof.

By the representation theorem [19, pp. 98-103] there exists an asymptotically stable filter which will produce a realization of $\{x_n\}$ when driven by white noise, and we have $Re^{j\omega} = H(e^{j\omega})H(e^{-j\omega})$ . We define the analytic continuation of $Re^{j\omega}$ by $R(z) = H(z)H(z^{-1})$ . Decomposing into a sum of causal and anti-causal components gives

$\begin{eqnarray*} R(z) = \frac{b(z)b(z^{-1})}{ a(z)a(z^{-1})} &=&R_+(z) + R_-(z) \\ &=& \frac{q(z)}{ a(z)}+\frac{q(z^{-1})}{ a(z^{-1})} \end{eqnarray*}$

where is found by equating coefficients of like powers of in

$\displaystyle b(z)b(z^{-1})=q(z)a(z^{-1}) + a(z)q(z^{-1}).$

Since the poles of and are the same, it only remains to be shown that re $\left\{R_+(e^{j\omega})\right\}\geq 0,\;0\leq \omega\leq \pi$ .

Since spectral power is nonnegative, $Re^{j\omega}\geq 0$ for all $\omega$ , and so

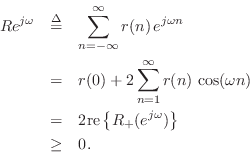
$\begin{eqnarray*} Re^{j\omega}&\isdef & \sum_{n=-\infty }^\infty r(n)\,e^{j\omeg... ...)\\ &=&2\mbox{re}\left\{R_+(e^{j\omega})\right\}\\ &\geq& 0. \end{eqnarray*}$

$\Box$

Relation to Schur Functions

Definition. A Schur function is defined as a complex function analytic and of modulus not exceeding unity in $\vert z\vert\leq 1$ .

Property. The function

$\displaystyle S(z) \isdef \frac{1-R(z)}{ 1+R(z)}$

(C.84)

is a Schur function if and only if

is positive real.

Proof.

Suppose is positive real. Then for $\vert z\vert\geq 1$ , re $\left\{R(z)\right\}\geq 0 \,\,\Rightarrow\,\,1+$ re $\left\{R(z)\right\}\geq 0 \,\,\Rightarrow\,\,1+R(z)$ is PR. Consequently, is minimum phase which implies all roots of lie in the unit circle. Thus is analytic in $\vert z\vert\leq 1$ . Also,

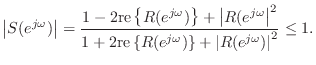
$\displaystyle \left\vert S(e^{j\omega})\right\vert = \frac{1-2\mbox{re}\left\{R... ...left\{R(e^{j\omega})\right\} + \left\vert R(e^{j\omega})\right\vert^2} \leq 1.$

By the maximum modulus theorem,

takes on its maximum value in $\vert z\vert\geq 1$ on the boundary. Thus

is Schur.

Conversely, suppose is Schur. Solving Eq. $\,$ (C.84) for and taking the real part on the unit circle yields

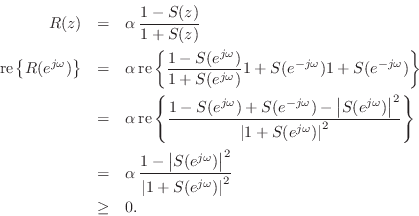
$\begin{eqnarray*} R(z) &=& \alpha\,\frac{1-S(z)}{ 1+S(z)} \\ \mbox{re}\left\{R(... ...ert^2 }{ \left\vert 1+S(e^{j\omega})\right\vert^2}\\ &\geq& 0. \end{eqnarray*}$

If $S(z)=\alpha$ is constant, then $R(z)=(1-\vert\alpha\vert^2)/\vert 1+\alpha\vert^2$ is PR. If is not constant, then by the maximum principle, for $\vert z\vert>1$ . By Rouche's theorem applied on a circle of radius $1+\epsilon$ , $\epsilon>0$ , on which $\vert S(z)\vert<1$ , the function has the same number of zeros as the function in $\vert z\vert\geq 1+\epsilon$ . Hence, is minimum phase which implies is analytic for $z\geq 1$ . Thus is PR. $\Box$

Relation to functions positive real in the right-half plane

Property. re $\left\{H(z)\right\}\geq 0$ for $\left\vert z\right\vert\geq 1$ whenever

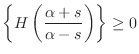
re $\displaystyle \left\{H\left(\frac{\alpha+s}{ \alpha-s}\right)\right\}\geq 0$

for re $\left\{s\right\}\geq 0$ , where $\alpha$ is any positive real number.

Proof. We shall show that the change of variable $z\leftarrow (\alpha+s)/(\alpha-s),\; \alpha>0$ , provides a conformal map from the z-plane to the s-plane that takes the region $\left\vert z\right\vert\geq 1$ to the region re $\left\{s\right\}\geq 0$ . The general formula for a bilinear conformal mapping of functions of a complex variable is given by

$\displaystyle \frac{(z-z_1)(z_2-z_3)}{ (z-z_3)(z_2-z_1)} = \frac{(s-s_1)(s_2-s_3)}{ (s-s_3)(s_2-s_1)}.$

(C.85)

In general, a bilinear transformation maps circles and lines into circles and lines [83]. We see that the choice of three specific points and their images determines the mapping for all and . We must have that the imaginary axis in the s-plane maps to the unit circle in the z-plane. That is, we may determine the mapping by three points of the form $z_i=e^{j\theta_i}$ and $s_i=j\omega_i,\;i=1,2,3$ . If we predispose one such mapping by choosing the pairs $(s_1=\pm\infty ) \leftrightarrow (z_1= -1)$ and $(s_3=0)\leftrightarrow(z_3=1)$ , then we are left with transformations of the form

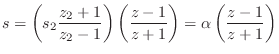
$\displaystyle s=\left(s_2 \frac{z_2+1}{ z_2-1}\right)\left( \frac{z-1}{ z+1}\right) =\alpha\left( \frac{z-1}{ z+1}\right)$

$\displaystyle z\leftarrow \frac{\alpha+s}{ \alpha-s},$

(C.86)

Letting

be some point $j\omega$ on the imaginary axis, and

be some point $e^{j\theta}$ on the unit circle, we find that

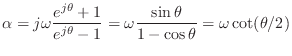
$\displaystyle \alpha = j\omega \frac{e^{j\theta} + 1}{ e^{j\theta} -1 } = \omega \frac{\sin\theta}{ 1-\cos\theta} = \omega\cot(\theta/2)$

which gives us that $\alpha$ is real. To avoid degeneracy, we require $s_2\neq 0,\infty ,\;z_2\neq \pm1$ , and this translates to $\alpha$ finite and nonzero. Finally, to make the unit disk map to the left-half s-plane, $\omega$ and $\theta$ must have the same sign in which case $\alpha>0$ . $\Box$

There is a bonus associated with the restriction that $\alpha$ be real which is that

$\displaystyle z= \frac{\alpha+s}{ \alpha-s}\in\Re \quad \leftrightarrow \quad s = \alpha \frac{z-1}{ z+1}\in\Re .$

(C.87)

We have therefore proven

Property.

$\displaystyle H(z)$ PR $\displaystyle \;\Leftrightarrow\;H\left(\frac{\alpha+s}{\alpha-s}\right)$ PR $\displaystyle , \protect$

where $\alpha$ is any positive real number.

The class of mappings of the form Eq. $\,$ (C.85) which take the exterior of the unit circle to the right-half plane is larger than the class Eq. $\,$ (C.86). For example, we may precede the transformation Eq. $\,$ (C.86) by any conformal map which takes the unit disk to the unit disk, and these mappings have the algebraic form of a first order complex allpass whose zero lies inside the unit circle.

$\displaystyle z\leftarrow e^{j\theta} \frac{w-w_0}{ \overline{w_0}\,w - 1},\qquad \left\vert w_0\right\vert<1$

(C.88)

where

is the zero of the allpass and the image (also pre-image) of the origin, and $\theta$ is an angle of pure rotation. Note that Eq. $\,$ (C.88) is equivalent to a pure rotation, followed by a real allpass substitution (

real), followed by a pure rotation. The general preservation of condition (2) in Def. 2 forces the real axis to map to the real axis. Thus rotations by other than $\pi$ are useless, except perhaps in some special cases. However, we may precede Eq. $\,$ (C.86) by the first order real allpass substitution

$\displaystyle z\leftarrow \frac{w-r}{ r\,w - 1},\qquad \left\vert r\right\vert<1,\; r$ real $\displaystyle , \protect$

which maps the real axis to the real axis. This leads only to the composite transformation,

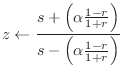
$\displaystyle z \leftarrow \frac{s+ \left(\alpha \frac{1-r}{1+r}\right)}{ s- \left(\alpha \frac{1-r}{1+r}\right)}$

which is of the form Eq. $\,$ (C.86) up to a minus sign (rotation by $\pi$ ). By inspection of Eq. $\,$ (C.85), it is clear that sign negation corresponds to the swapping of points

and

, or

and

. Thus the only extension we have found by means of the general disk to disk pre-transform, is the ability to interchange two of the three points already tried. Consequently, we conclude that the largest class of bilinear transforms which convert functions positive real in the outer disk to functions positive real in the right-half plane is characterized by

$\displaystyle z \leftarrow \pm \frac{\alpha+s}{ \alpha-s}.$

(C.89)

Riemann's theorem may be used to show that Eq. $\,$ (C.89) is also the largest such class of conformal mappings. It is not essential, however, to restrict attention solely to conformal maps. The pre-transform $z\leftarrow \overline{z}$ , for example, is not conformal and yet PR is preserved.

The bilinear transform is one which is used to map analog filters into digital filters. Another such mapping is called the matched transform [362]. It also preserves the positive real property.

Property. is PR if $H(e^{sT})$ is positive real in the analog sense, where is interpreted as the sampling period.

Proof. The mapping $z \leftarrow e^{sT}$ takes the right-half -plane to the outer disk in the -plane. Also is real if is real. Hence $H(e^{sT})$ PR implies PR. (Note, however, that rational functions do not in general map to rational functions.) $\Box$

These transformations allow application of the large battery of tests which exist for functions positive real in the right-half plane [524].

Special cases and examples

The sum of positive real functions is positive real.
The difference of positive real functions is conditionally positive real.
The product or division of positive real functions is conditionally PR.
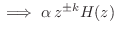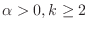PR $\implies \alpha\,z^{\pm k}H(z)$ not PR for $\alpha>0,k\geq 2$ .

Minimum Phase (MP) polynomials in

All properties of MP polynomials apply without modification to marginally stable allpole transfer functions (cf. Property 2):

Every first-order MP polynomial is positive real.
Every first-order MP polynomial 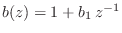$b(z)=1+b_1\,z^{-1}$ is such that 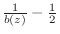$\frac{1}{ b(z)} - \frac{1}{ 2}$ is positive real.
A PR second-order MP polynomial with complex-conjugate zeros,

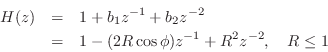
$\begin{eqnarray*} H(z)&=& 1+b_1z^{-1}+b_2z^{-2}\\ &=& 1-(2R\cos\phi)z^{-1}+R^2z^{-2},\quad R\leq 1 \end{eqnarray*}$

satisfies

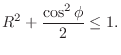
$\displaystyle R^2 + \frac{\cos^2\phi}{ 2} \leq 1.$
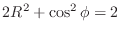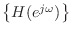If $2R^2+\cos^2\phi=2$ , then re $\left\{H(e^{j\omega})\right\}$ has a double zero at

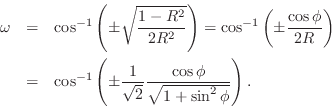
$\begin{eqnarray*} \omega &=& \cos^{-1}\left(\pm \sqrt{ \frac{1-R^2}{ 2R^2}}\righ... ...frac{1}{ \sqrt{2}} \frac{\cos\phi}{ \sqrt{1+\sin^2\phi}}\right). \end{eqnarray*}$
All polynomials of the form

$\displaystyle H(z)=1+R^nz^{-n},\quad R\leq 1$
are positive real. (These have zeros uniformly distributed on a circle of radius .)

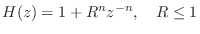
Miscellaneous Properties

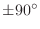If all poles and zeros of a PR function are on the unit circle, then they alternate along the circle. Since this property is preserved by the bilinear transform, it is true in both the and planes. It can be viewed as a consequence of the $\pm 90\degrees$ phase bounds for positive-real functions.
If 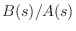is PR, then so is 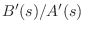$B^\prime(s)/A^\prime(s)$ , where the prime denotes differentiation in .