Piano Hammer Modeling
The previous section treated an ideal point-mass striking an ideal string. This can be considered a simplified piano-hammer model. The model can be improved by adding a damped spring to the point-mass, as shown in Fig.9.22 (cf. Fig.9.12).
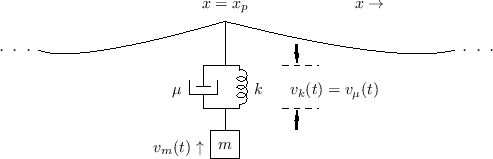 |
The impedance of this plucking system, as seen by the string, is the
parallel combination of the mass impedance ![]() and the damped spring
impedance
and the damped spring
impedance ![]() . (The damper
. (The damper ![]() and spring
and spring ![]() are formally
in series--see §7.2, for a refresher on series versus
parallel connection.) Denoting
the driving-point impedance of the hammer at the string contact-point
by
are formally
in series--see §7.2, for a refresher on series versus
parallel connection.) Denoting
the driving-point impedance of the hammer at the string contact-point
by ![]() , we have
, we have
Thus, the scattering filters in the digital waveguide model are second order (biquads), while for the string struck by a mass (§9.3.1) we had first-order scattering filters. This is expected because we added another energy-storage element (a spring).
The impedance formulation of Eq.![]() (9.19) assumes all elements are
linear and time-invariant (LTI), but in practice one can normally
modulate element values as a function of time and/or state-variables
and obtain realistic results for low-order elements. For this we must
maintain filter-coefficient formulas that are explicit functions of
physical state and/or time. For best results, state variables should
be chosen so that any nonlinearities remain memoryless in the
digitization
[361,348,554,555].
(9.19) assumes all elements are
linear and time-invariant (LTI), but in practice one can normally
modulate element values as a function of time and/or state-variables
and obtain realistic results for low-order elements. For this we must
maintain filter-coefficient formulas that are explicit functions of
physical state and/or time. For best results, state variables should
be chosen so that any nonlinearities remain memoryless in the
digitization
[361,348,554,555].
Nonlinear Spring Model
In the musical acoustics literature, the piano hammer is classically
modeled as a nonlinear spring
[493,63,178,76,60,486,164].10.14Specifically, the piano-hammer damping in Fig.9.22 is
typically approximated by ![]() , and the spring
, and the spring ![]() is
nonlinear and memoryless according to a simple power
law:
is
nonlinear and memoryless according to a simple power
law:

The upward force applied to the string by the hammer is therefore
| (10.20) |
This force is balanced at all times by the downward string force (string tension times slope difference), exactly as analyzed in §9.3.1 above.
Including Hysteresis
Since the compressed hammer-felt (wool) on real piano hammers shows significant hysteresis memory, an improved piano-hammer felt model is
where
Equation (9.21) is said to be a good approximation under normal playing conditions. A more complete hysteresis model is [487]
![$\displaystyle f_h(t) \eqsp f_0\left[x_k^p(t) - \frac{\epsilon}{\tau_0} \int_0^t x_k^p(\xi) \exp\left(\frac{\xi-t}{\tau_0}\right)d\xi\right]
$](http://www.dsprelated.com/josimages_new/pasp/img2179.png)

Relating to Eq.![]() (9.21) above, we have
(9.21) above, we have
![]() (N/mm
(N/mm![]() ).
).
Piano Hammer Mass
The piano-hammer mass may be approximated across the keyboard by [487]
Next Section:
Pluck Modeling
Previous Section:
Ideal String Struck by a Mass








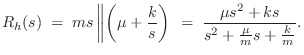
![$\displaystyle f_h(t) \eqsp Q_0\left[x_k^p + \alpha \frac{d(x_k^p)}{dt}\right], \protect$](http://www.dsprelated.com/josimages_new/pasp/img2177.png)











