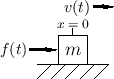State-Space Model of a Force-Driven Mass
For the simple example of a mass ![]() driven by external force
driven by external force ![]() along the
along the ![]() axis, we have the system of Fig.1.6.
We should choose the state variable to be velocity
axis, we have the system of Fig.1.6.
We should choose the state variable to be velocity
![]() so that
Newton's
so that
Newton's ![]() yields
yields
Next Section:
Numerical Integration of General State-Space Models
Previous Section:
Forming Outputs