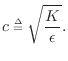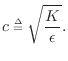Free Books
   Free Books    Physical Audio Signal Processing  

Traveling-Wave Solution

It can be readily checked (see §C.3 for details) that the lossless 1D wave equation

$\displaystyle Ky''= \epsilon {\ddot y}$

(where all terms are defined in Eq.$ \,$(6.1)) is solved by any string shape which travels to the left or right with speed

$\displaystyle c \isdeftext \sqrt{\frac{K}{\epsilon }}. $

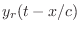
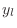
If we denote right-going traveling waves in general by $ y_r(t-x/c)$ and left-going traveling waves by $ y_l(t+x/c)$, where $ y_r$ and $ y_l$ are arbitrary twice-differentiable functions, then the general class of solutions to the lossless, one-dimensional, second-order wave equation can be expressed as

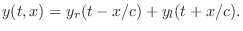$\displaystyle y(t,x) = y_r(t-x/c) + y_l(t+x/c). \protect$ (7.2)

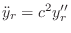
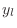
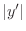
Note that we have $ {\ddot y}_r= c^2y''_r$ and $ {\ddot y}_l= c^2y''_l$ (derived in §C.3.1) showing that the wave equation is satisfied for all traveling wave shapes $ y_r$ and $ y_l$. However, the derivation of the wave equation itself assumes the string slope $ \vert y^\prime\vert$ is much less than $ 1$ at all times and positions (see §B.6). An important point to note is that a function of two variables $ y(t,x)$ is replaced by two functions of a single (time) variable. This leads to great reductions in computational complexity, as we will see. The traveling-wave solution of the wave equation was first published by d'Alembert in 1747 [100]7.1

Next Section:
Sampled Traveling-Wave Solution
Previous Section:
Wave Equation Applications