DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Traveling-Wave Solution

It is easily shown that the lossless 1D wave equation $ Ky''=\epsilon {\ddot y}$ is solved by any string shape which travels to the left or right with speed $ c \isdeftext \sqrt{K/\epsilon }$. Denote right-going traveling waves in general by $ y_r(t-x/c)$ and left-going traveling waves by $ y_l(t+x/c)$, where $ y_r$ and $ y_l$ are assumed twice-differentiable.C.1Then a general class of solutions to the lossless, one-dimensional, second-order wave equation can be expressed as

$\displaystyle y(t,x) = y_r\left(t-\frac{x}{c}\right) + y_l\left(t+\frac{x}{c}\right). \protect$ (C.11)

The next section derives the result that $ {\ddot y}_r= c^2y''_r$ and $ {\ddot y}_l= c^2y''_l$, establishing that the wave equation is satisfied for all traveling wave shapes $ y_r$ and $ y_l$. However, remember that the derivation of the wave equation in §B.6 assumes the string slope is much less than $ 1$ at all times and positions. Finally, we show in §C.3.6 that the traveling-wave picture is general; that is, any physical state of the string can be converted to a pair of equivalent traveling force- or velocity-wave components.

An important point to note about the traveling-wave solution of the 1D wave equation is that a function of two variables $ y(t,x)$ has been replaced by two functions of a single variable in time units. This leads to great reductions in computational complexity.

The traveling-wave solution of the wave equation was first published by d'Alembert in 1747 [100]. See Appendix A for more on the history of the wave equation and related topics.

Traveling-Wave Partial Derivatives

Because we have defined our traveling-wave components $ y_r(t-x/c)$ and $ y_l(t+x/c)$ as having arguments in units of time, the partial derivatives with respect to time $ t$ are identical to simple derivatives of these functions. Let $ {\dot y}_r$ and $ {\dot y}_l$ denote the (partial) derivatives with respect to time of $ y_r$ and $ y_l$, respectively. In contrast, the partial derivatives with respect to $ x$ are

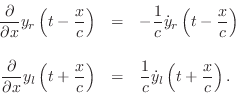
\begin{eqnarray*} \frac{\partial}{\partial x} y_r\left(t-\frac{x}{c}\right) &=&... ...c}\right) &=& \frac{1}{c}{\dot y}_l\left(t+ \frac{x}{c}\right). \end{eqnarray*}

Denoting the spatial partial derivatives by $ y'_r$ and $ y'_l$, respectively, we can write more succinctly

\begin{eqnarray*} y'_r&=& -\frac{1}{c}{\dot y}_r\\ [5pt] y'_l&=& \frac{1}{c}{\dot y}_l, \end{eqnarray*}

where this argument-free notation assumes the same $ t$ and $ x$ for all terms in each equation, and the subscript $ l$ or $ r$ determines whether the omitted argument is $ t + x/c$ or $ t - x/c$.

Now we can see that the second partial derivatives in $ x$ are

\begin{eqnarray*} y''_r&=& \left(-\frac{1}{c}\right)^2 {\ddot y}_r= \frac{1}{c^2... ...eft(\frac{1}{c}\right)^2 {\ddot y}_l= \frac{1}{c^2} {\ddot y}_l. \end{eqnarray*}

These relations, together with the fact that partial differention is a linear operator, establish that

$\displaystyle y(t,x) = y_r\left(t-\frac{x}{c}\right) + y_l\left(t+\frac{x}{c}\right). \protect$

obeys the ideal wave equation $ {\ddot y}= c^2y''$ for all twice-differentiable functions $ y_r$ and $ y_l$.

Use of the Chain Rule

These traveling-wave partial-derivative relations may be derived a bit more formally by means of the chain rule from calculus, which states that, for the composition of functions $ f$ and $ g$, i.e.,

$\displaystyle y(x) = f(g(x)), $

the derivative of the composition with respect to $ x$ can be expressed according to the chain rule as

$\displaystyle y'(x) = f^\prime(g(x))g^\prime(x), $

where $ f^\prime(x)$ denotes the derivative of $ f(x)$ with respect to $ x$.

To apply the chain rule to the spatial differentiation of traveling waves, define

\begin{eqnarray*} g_r(t,x) &=& t - \frac{x}{c}\\ [10pt] g_l(t,x) &=& t + \frac{x}{c}. \end{eqnarray*}

Then the traveling-wave components can be written as $ y_r[g_r(t,x)]$ and $ y_l[g_l(t,x)]$, and their partial derivatives with respect to $ x$ become

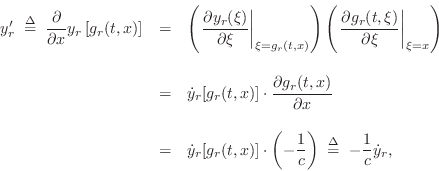
\begin{eqnarray*} y'_r\;\isdef \; \frac{\partial}{\partial x} y_r\left[g_r(t,x)\... ...t \left(-\frac{1}{c}\right) \;\isdef \; -\frac{1}{c}{\dot y}_r, \end{eqnarray*}

and similarly for $ y'_l$.

String Slope from Velocity Waves

Let's use the above result to derive the slope of the ideal vibrating string From Eq.$ \,$(C.11), we have the string displacement given by

$\displaystyle y(t,x) = y_r(t-x/c) + y_l(t+x/c). \protect$

By linearity of differentiation, the string slope is given by

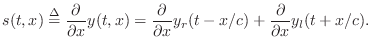
$\displaystyle s(t,x) \isdef \frac{\partial}{\partial x} y(t,x) = \frac{\partial}{\partial x}y_r(t-x/c) + \frac{\partial}{\partial x}y_l(t+x/c). $

Consider only the right-going component, and define

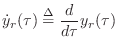
$\displaystyle {\dot y}_r(\tau) \isdef \frac{d}{d\tau} y_r(\tau) $

with $ \tau\isdef t-x/c$. By the chain rule,

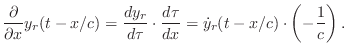
$\displaystyle \frac{\partial}{\partial x}y_r(t-x/c) = \frac{dy_r}{d\tau} \cdot \frac{d\tau}{dx} = {\dot y}_r(t-x/c)\cdot\left(-\frac{1}{c}\right). $

The left-going component is similar, but with $ +1/c$. Thus, the string slope in terms of traveling velocity-wave components can be written as

$\displaystyle s(t,x) = \frac{1}{c}{\dot y}_l(t+x/c) - \frac{1}{c}{\dot y}_r(t-x/c). $

Wave Velocity

Because $ e^{st}$ is an eigenfunction under differentiation (i.e., the exponential function is its own derivative), it is often profitable to replace it with a generalized exponential function, with maximum degrees of freedom in its parametrization, to see if parameters can be found to fulfill the constraints imposed by differential equations.

In the case of the one-dimensional ideal wave equation (Eq.$ \,$(C.1)), with no boundary conditions, an appropriate choice of eigensolution is

$\displaystyle y(t,x) = e^{st+vx}$ (C.12)

Substituting into the wave equation yields

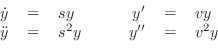
\begin{displaymath} \begin{array}{rclcrcl} {\dot y}& \,\mathrel{\mathop=}\,& sy... ...\quad & y''& \,\mathrel{\mathop=}\,& v^2y \nonumber \end{array}\end{displaymath}

Defining the wave velocity (or phase velocityC.2) as $ c \isdeftext {s/v}$, the wave equation becomes
$\displaystyle Kv^2y$ $\displaystyle =$ $\displaystyle \epsilon s^2y$ (C.13)
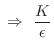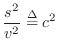$\displaystyle \,\,\Rightarrow\,\,\frac{K}{\epsilon }$ $\displaystyle =$ $\displaystyle \frac{s^2}{v^2} \isdef c^2$  
$\displaystyle \,\,\Rightarrow\,\,v$ $\displaystyle =$ $\displaystyle \pm \frac{s}{c}.$  

Thus

$\displaystyle y(t,x) = e^{s(t\pm x/c)} $

is a solution for all $ s$. By superposition,

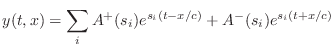
$\displaystyle y(t,x) = \sum\limits_i^{} A^{+}(s_i) e^{s_i(t-x/c)}+ A^{-}(s_i) e^{s_i(t+x/c)} $

is also a solution, where $ A^{+}(s_i)$ and $ A^{-}(s_i)$ are arbitrary complex-valued functions of arbitrary points $ s_i$ in the complex plane.

D'Alembert Derived

Setting $ s\isdeftext j \omega $, and extending the summation to an integral, we have, by Fourier's theorem,

$\displaystyle y(t,x) = y_r\left(t-\frac{x}{c}\right) + y_l\left(t+\frac{x}{c}\right)$ (C.14)

for arbitrary continuous functions $ y_r(\cdot)$ and $ y_l(\cdot)$. This is again the traveling-wave solution of the wave equation attributed to d'Alembert, but now derived from the eigen-property of sinusoids and Fourier theory rather than ``guessed''.

An example of the appearance of the traveling wave components shortly after plucking an infinitely long string at three points is shown in Fig.C.2.

Figure C.2: An infinitely long string, ``plucked'' simultaneously at three points, labeled ``p'' in the figure, so as to produce an initial triangular displacement. The initial displacement is modeled as the sum of two identical triangular pulses which are exactly on top of each other at time 0. At time $ t_0$ shortly after time 0, the traveling waves centers are separated by $ 2ct_0$ meters, and their sum gives the trapezoidal physical string displacement at time $ t_0$ which is also shown. Note that only three short string segments are in motion at that time: the flat top segment which is heading to zero where it will halt forever, and two short pieces on the left and right which are the leading edges of the left- and right-going traveling waves. The string is not moving where the traveling waves overlap at the same slope. When the traveling waves fully separate, the string will be at rest everywhere but for two half-amplitude triangular pulses heading off to plus and minus infinity at speed $ c$.
\includegraphics[width=\twidth]{eps/f_t_waves_no_term}

Converting Any String State to Traveling Slope-Wave Components

We verified in §C.3.1 above that traveling-wave components $ y_r$ and $ y_l$ in Eq.$ \,$(C.14) satisfy the ideal string wave equation $ {\ddot y}= c^2y''$. By definition, the physical string displacement is given by the sum of the traveling-wave components, or

$\displaystyle y(t,x) \eqsp y_r\left(t-\frac{x}{c}\right) + y_l\left(t+\frac{x}{c}\right). \protect$ (C.15)

Thus, given any pair of traveling waves $ y_r$ and $ y_l$, we can compute a corresponding string displacement $ y$. This leads to the question whether any initial string state can be converted to a pair of equivalent traveling-wave components. If so, then d'Alembert's traveling-wave solution is complete, and all solutions to the ideal string wave equation can be expressed in terms of traveling waves.

The state of an ideal string at time $ t$ is classically specified by its displacement $ y(t,x)$ and velocity

$\displaystyle v(t,x)\isdefs {\dot y}(t,x)\isdefs \frac{\partial}{\partial t} y(t,x) $

for all $ x$ [317]. Equation (C.15) gives us $ y$ as a simple sum of the traveling-wave components, and now we need a formula for $ v$ in terms of them as well. It will be derived in §C.7.3 (see Equations (C.44-C.46)) that we can write

$\displaystyle v(t,x) \eqsp -cy_r^\prime\left(t-\frac{x}{c}\right) + cy_l^\prime\left(t+\frac{x}{c}\right). $

where $ y'$ denotes the partial derivative with respect to $ x$ as usual. We have

$\displaystyle \left[\begin{array}{c} y(t,x) \\ [2pt] v(t,x) \end{array}\right] ... ...ght] \left[\begin{array}{c} y_r(t-x/c) \\ [2pt] y_l(t+x/c) \end{array}\right]. $

Inverting the two-by-two differential operator matrix yields left- and right-going slope waves as a function of an arbitrary initial slope and velocity:

$\displaystyle \left[\begin{array}{c} y'^{+} \\ [2pt] y'^{-} \end{array}\right] ... ...eft[\begin{array}{c} y'-\frac{v}{c} \\ [2pt] y'+\frac{v}{c} \end{array}\right] $

Integrating both sides with respect to $ x$, and choosing the constant of integration to give the correct constant component of $ y$, we obtain the displacement-wave components

$\displaystyle \left[\begin{array}{c} y^{+} \\ [2pt] y^{-} \end{array}\right] \eqsp \frac{1}{2}\left[\begin{array}{c} y-w \\ [2pt] y+w \end{array}\right] $

where

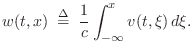
$\displaystyle w(t,x) \isdefs \frac{1}{c}\int_{-\infty}^x v(t,\xi)\,d\xi. $

Notice that if the initial velocity is zero, each of the initial traveling displacement waves is simply half the initial displacement, as expected. On the other hand, if the initial displacement is zero and there is a uniform initial velocity (the whole string is moving), the initial displacement-wave components are unbounded as the string length goes to infinity. Related discussion appears in Appendix E.

It will be seen in §C.7.4 that state conversion between physical variables and traveling-wave components is simpler when force and velocity are chosen as the physical state variables (as opposed to displacement and velocity used here).

Next Section:
Sampled Traveling Waves
Previous Section:
The Finite Difference Approximation