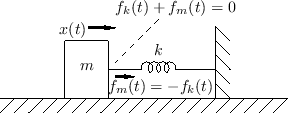Newton's Laws of Motion
Perhaps the most heavily used equation in physics is Newton's second law of motion:
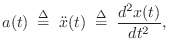
In this formulation, the applied force
Newton's Three Laws of Motion
Newton's three laws of motion may be stated as follows:
- Every object in a state of uniform motion will remain in that
state of motion unless an external force acts on it.
- Force equals mass times acceleration [
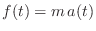 ].
].
- For every action there is an equal and opposite reaction.
The first law, also called the law of inertia, was pioneered by Galileo. This was quite a conceptual leap because it was not possible in Galileo's time to observe a moving object without at least some frictional forces dragging against the motion. In fact, for over a thousand years before Galileo, educated individuals believed Aristotle's formulation that, wherever there is motion, there is an external force producing that motion.
The second law,
![]() , actually implies the first law, since
when
, actually implies the first law, since
when ![]() (no applied force), the acceleration
(no applied force), the acceleration ![]() is zero,
implying a constant velocity
is zero,
implying a constant velocity ![]() . (The velocity is simply the
integral with respect to time of
. (The velocity is simply the
integral with respect to time of
![]() .)
.)
Newton's third law implies conservation of momentum [137]. It can also be seen as following from the second law: When one object ``pushes'' a second object at some (massless) point of contact using an applied force, there must be an equal and opposite force from the second object that cancels the applied force. Otherwise, there would be a nonzero net force on a massless point which, by the second law, would accelerate the point of contact by an infinite amount.
In summary, Newton's laws boil down to ![]() . An enormous quantity
of physical science has been developed by applying this
simpleB.1 mathematical law to different physical
situations.
. An enormous quantity
of physical science has been developed by applying this
simpleB.1 mathematical law to different physical
situations.
Mass
Mass is an intrinsic property of matter.
From Newton's second law,
![]() , we have that the amount of
force required to accelerate an object, by a given amount, is
proportional to its mass. Thus, the mass of an object quantifies its
inertia--its resistance to a change in velocity.
, we have that the amount of
force required to accelerate an object, by a given amount, is
proportional to its mass. Thus, the mass of an object quantifies its
inertia--its resistance to a change in velocity.
We can measure the mass of an object by measuring the
gravitational force between it and another known mass,
as described in the next section. This is a special case of measuring
its acceleration in response to a known force. Whatever the force ![]() ,
the mass
,
the mass ![]() is given by
is given by ![]() divided by the resulting acceleration
divided by the resulting acceleration
![]() , again by Newton's second law
, again by Newton's second law ![]() .
.
The usual mathematical model for an ideal mass is a dimensionless point at some location in space. While no real objects are dimensionless, they can often be treated mathematically as dimensionless points located at their center of mass, or centroid (§B.4.1).
The physical state of a mass ![]() at time
at time ![]() consists of its
position
consists of its
position ![]() and velocity
and velocity
![]() in 3D space.
The amount of mass itself,
in 3D space.
The amount of mass itself, ![]() , is regarded as a fixed parameter that
does not change. In other words, the state
, is regarded as a fixed parameter that
does not change. In other words, the state
![]() of a
physical system typically changes over time, while any
parameters of the system, such as mass
of a
physical system typically changes over time, while any
parameters of the system, such as mass ![]() , remain fixed over
time (unless otherwise specified).
, remain fixed over
time (unless otherwise specified).
Gravitational Force
We are all familiar with the force of gravity. It is a
fundamental observed property of our universe that any two masses
![]() and
and ![]() experience an attracting force
experience an attracting force ![]() given by the
formula
given by the
formula
where
The law of gravitation Eq.![]() (B.2) can be accepted as an
experimental fact which defines the concept of a force.B.3 The giant conceptual leap taken by Newton was that the law of
gravitation is
universal--applying to celestial bodies as well as objects on
earth. When a mass is ``dropped'' and allowed to ``fall'' in a
gravitational field, it is observed to experience a
uniform acceleration proportional to its mass. Newton's second
law of motion (§B.1) quantifies this result.
(B.2) can be accepted as an
experimental fact which defines the concept of a force.B.3 The giant conceptual leap taken by Newton was that the law of
gravitation is
universal--applying to celestial bodies as well as objects on
earth. When a mass is ``dropped'' and allowed to ``fall'' in a
gravitational field, it is observed to experience a
uniform acceleration proportional to its mass. Newton's second
law of motion (§B.1) quantifies this result.
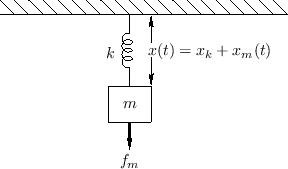
Hooke's Law
Consider an ideal spring suspending a mass from a rigid ceiling, as
depicted in Fig.B.1. Assume the mass is at rest,
and that its distance ![]() from the ceiling is fixed.
from the ceiling is fixed.
If ![]() denotes the mass of the earth, and
denotes the mass of the earth, and ![]() is the distance of mass
is the distance of mass
![]() 's center from the earth's center of mass, then the downward force
on the mass
's center from the earth's center of mass, then the downward force
on the mass ![]() is given by Eq.
is given by Eq.![]() (B.2) as
(B.2) as
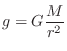
where
Note that the force on the spring in Fig.B.1 is gravitational force. Equal and opposite to the force of gravity is the spring force exerted upward by the spring on the mass (which is not moving). We know that the spring force is equal and opposite to the gravitational force because the mass would otherwise be accelerated by the net force.B.4 Therefore, like gravity, a displaced spring can be regarded as a definition of an applied force. That is, whenever you have to think of an applied force, you can always consider it as being delivered by the end of some ideal spring attached to some external physical system.
Note, by the way, that normal interaction forces when objects touch arise from the Coulomb force (electrostatic force, or repulsion of like charges) between electron orbitals. This electrostatic force obeys an ``inverse square law'' like gravity, and therefore also behaves like an ideal spring for small displacements.B.5
The specific value of ![]() depends on the physical units adopted as
well as the ``stiffness'' of the spring. What is most important in
this definition of force is that a doubling of spring displacement
doubles the force. That is, the spring force is a linear
function of spring displacement (compression or stretching).
depends on the physical units adopted as
well as the ``stiffness'' of the spring. What is most important in
this definition of force is that a doubling of spring displacement
doubles the force. That is, the spring force is a linear
function of spring displacement (compression or stretching).
Applying Newton's Laws of Motion
As a simple example, consider a mass ![]() driven along a frictionless
surface by an ideal spring
driven along a frictionless
surface by an ideal spring ![]() , as shown in Fig.B.2.
Assume that the mass position
, as shown in Fig.B.2.
Assume that the mass position ![]() corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance
corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance ![]() is given by Hooke's law (§B.1.3):
is given by Hooke's law (§B.1.3):
where we have defined
where
Next Section:
Work = Force times Distance = Energy
Previous Section:
Summary