Example of Overlap-Add Convolution
Let's look now at a specific example of FFT convolution:
- Impulse-train test signal, 4000 Hz sampling-rate
- Length
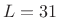 causal lowpass filter, 600 Hz cut-off
causal lowpass filter, 600 Hz cut-off
- Length
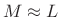 rectangular window
rectangular window
- Hop size
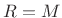 (no overlap)
(no overlap)
We will work through the matlab for this example and display the results. First, the simulation parameters:
L = 31; % FIR filter length in taps fc = 600; % lowpass cutoff frequency in Hz fs = 4000; % sampling rate in Hz Nsig = 150; % signal length in samples period = round(L/3); % signal period in samplesFFT processing parameters:
M = L; % nominal window length Nfft = 2^(ceil(log2(M+L-1))); % FFT Length M = Nfft-L+1 % efficient window length R = M; % hop size for rectangular window Nframes = 1+floor((Nsig-M)/R); % no. complete framesGenerate the impulse-train test signal:
sig = zeros(1,Nsig); sig(1:period:Nsig) = ones(size(1:period:Nsig));Design the lowpass filter using the window method:
epsilon = .0001; % avoids 0 / 0 nfilt = (-(L-1)/2:(L-1)/2) + epsilon; hideal = sin(2*pi*fc*nfilt/fs) ./ (pi*nfilt); w = hamming(L); % FIR filter design by window method h = w' .* hideal; % window the ideal impulse response hzp = [h zeros(1,Nfft-L)]; % zero-pad h to FFT size H = fft(hzp); % filter frequency responseCarry out the overlap-add FFT processing:
y = zeros(1,Nsig + Nfft); % allocate output+'ringing' vector
for m = 0:(Nframes-1)
index = m*R+1:min(m*R+M,Nsig); % indices for the mth frame
xm = sig(index); % windowed mth frame (rectangular window)
xmzp = [xm zeros(1,Nfft-length(xm))]; % zero pad the signal
Xm = fft(xmzp);
Ym = Xm .* H; % freq domain multiplication
ym = real(ifft(Ym)) % inverse transform
outindex = m*R+1:(m*R+Nfft);
y(outindex) = y(outindex) + ym; % overlap add
end
The time waveforms for the first three frames (![]() ) are shown in
Figures 8.12 through 8.14. Notice how the causal linear-phase filtering results
in an overall signal delay by half the filter length. Also, note how
frames 0 and 2 contain four impulses, while frame 1 only happens to
catch three; this causes no difficulty, and the filtered result remains
correct by superposition.
) are shown in
Figures 8.12 through 8.14. Notice how the causal linear-phase filtering results
in an overall signal delay by half the filter length. Also, note how
frames 0 and 2 contain four impulses, while frame 1 only happens to
catch three; this causes no difficulty, and the filtered result remains
correct by superposition.
Next Section:
Summary of Overlap-Add FFT Processing
Previous Section:
Acyclic Convolution








![\includegraphics[width=0.8\twidth]{eps/ola0}](http://www.dsprelated.com/josimages_new/sasp2/img1443.png)
![\includegraphics[width=0.8\twidth]{eps/ola1}](http://www.dsprelated.com/josimages_new/sasp2/img1444.png)
![\includegraphics[width=0.8\twidth]{eps/ola2}](http://www.dsprelated.com/josimages_new/sasp2/img1445.png)











