DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

The Bilinear Transform

The formula for a general first-order (bilinear) conformal mapping of functions of a complex variable is conveniently expressed by [42, page 75]

$\displaystyle {(\zeta -\zeta _1)(\zeta _2-\zeta _3) \over (\zeta _2-\zeta _1)(\zeta -\zeta _3)} = {(z-z_1)(z_2-z_3) \over (z_2-z_1)(z-z_3)}. $

It can be seen that choosing three specific points and their images determines the mapping for all $ z$ and $ \zeta $ .

Bilinear transformations map circles and lines into circles and lines (lines being viewed as circles passing through the point at infinity). In digital audio, where both domains are ``$ z$ planes,'' we normally want to map the unit circle to itself, with dc mapping to dc ( $ z_1=\zeta _1=1$ ) and half the sampling rate mapping to half the sampling rate ( $ z_2=\zeta _2=-1$ ). Making these substitutions in (E.2) leaves us with transformations of the form

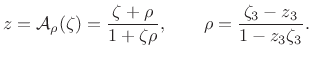$\displaystyle z= {\cal A}_{\rho }(\zeta ) = {\zeta + \rho \over 1 + \zeta \rho } , \qquad \rho = {\zeta _3 - z_3 \over 1 - z_3\zeta _3}.$ (E.1)

The constant $ \rho $ provides one remaining degree of freedom which can be used to map any particular frequency $ \omega$ (corresponding to the point $ e^{j\omega }$ on the unit circle) to a new location $ a(\omega )$ . All other frequencies will be warped accordingly. Note that this class of ``circle to circle'' bilinear transformations takes the form of the transfer function of an allpass filter. We therefore call it an ``allpass transformation''. The ``allpass coefficient'' $ \rho $ can be written in terms of the frequencies $ \omega$ and $ a(\omega )$ as

$\displaystyle \rho = {\sin\{[a(\omega )-\omega ]/2\} \over \sin\{[a(\omega )+\omega ]/2\} }.$ (E.2)

In this form, it is clear that $ \rho $ is real, and that the inverse of $ {\cal A}_{\rho }$ is $ {\cal A}_{-\rho }$ . Also, since $ 0\leq\{\omega ,a(\omega )\}\leq\pi$ , and $ a(\omega )\geq\omega $ for an audio warping (where low frequencies must be ``stretched out'' relative to high frequencies), we have $ \rho \in[0,1)$ for audio-type mappings from the $ z$ plane to the $ \zeta $ plane.

Next Section:
Optimal Bilinear Bark Warping
Previous Section:
The Bark Frequency Scale