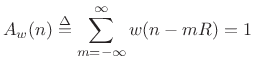Choice of Hop Size
A question related to the STFT analysis window is the hop size ![]() ,
i.e., how much we can advance the analysis time origin from frame to
frame. This depends very much on the purposes of the analysis. In
general, more overlap will give more analysis points and therefore
smoother results across time, but the computational expense is
proportionately greater. For purposes of spectrogram display or
additive synthesis parameter extraction, a conservative constraint
is to require that the analysis window overlap-add to a constant
at the chosen hop size:
,
i.e., how much we can advance the analysis time origin from frame to
frame. This depends very much on the purposes of the analysis. In
general, more overlap will give more analysis points and therefore
smoother results across time, but the computational expense is
proportionately greater. For purposes of spectrogram display or
additive synthesis parameter extraction, a conservative constraint
is to require that the analysis window overlap-add to a constant
at the chosen hop size:
where
The COLA constraint can be overly conservative for steady-state signals. For additive synthesis purposes, it is more efficient and still effective to increase the hop size to the number of samples over which the spectrum is not changing appreciably. In the case of the steady-state portion of piano tones, the hop size appears to be limited by the fastest amplitude envelope ``beat'' frequency caused by mistuning strings on one key or by overlapping partials from different keys.
For certain window types (such as sum-of-cosine windows, as discussed
in Chapter 3), there exist perfect overlap factors in the sense
of (H.1). For example, a rectangular window can hop by ![]() ,
where
,
where ![]() is any positive integer, and a Hanning or Hamming window can
use any hop size of the form
is any positive integer, and a Hanning or Hamming window can
use any hop size of the form ![]() . For the Kaiser window, in
contrast, there is no perfect hop size other than
. For the Kaiser window, in
contrast, there is no perfect hop size other than ![]() .
.
The COLA criterion for windows and their hop sizes is not the best
perspective to take when overlap-add synthesis is being constructed
from the modified spectra
![]() [7]. As discussed in Chapter 9, the hop size
[7]. As discussed in Chapter 9, the hop size ![]() is the
decimation factor applied to each FFT filter-bank output, and the
window is the envelope of each filter's impulse response. The
decimation by
is the
decimation factor applied to each FFT filter-bank output, and the
window is the envelope of each filter's impulse response. The
decimation by ![]() causes aliasing, and the frame rate
causes aliasing, and the frame rate ![]() is equal to twice the ``folding frequency'' of this aliasing.
Consequently, to minimize aliasing, the choice of hop size
is equal to twice the ``folding frequency'' of this aliasing.
Consequently, to minimize aliasing, the choice of hop size ![]() should
be such that the folding frequency exceeds the ``cut-off frequency'' of
the window. The cut-off frequency of a window can be defined as the
frequency above which the window transform magnitude is less than or
equal to the worst-case side-lobe level. For convenience, we typically
use the frequency of the first zero-crossing beyond the main lobe as
the definition of cut-off frequency. Following this rule yields
should
be such that the folding frequency exceeds the ``cut-off frequency'' of
the window. The cut-off frequency of a window can be defined as the
frequency above which the window transform magnitude is less than or
equal to the worst-case side-lobe level. For convenience, we typically
use the frequency of the first zero-crossing beyond the main lobe as
the definition of cut-off frequency. Following this rule yields ![]() overlap for the rectangular window,
overlap for the rectangular window, ![]() overlap for Hamming and
Hanning windows, and
overlap for Hamming and
Hanning windows, and ![]() (5/6) overlap for Blackman windows. The
hop size usable with a Kaiser window is determined by its design
parameters (principally, the desired time-bandwidth product of the
window, or, the ``beta'' parameter) [115].
(5/6) overlap for Blackman windows. The
hop size usable with a Kaiser window is determined by its design
parameters (principally, the desired time-bandwidth product of the
window, or, the ``beta'' parameter) [115].
One may wonder what happens to aliasing in the perfect-reconstruction case in which (H.1) is satisfied. The answer is that aliasing does occur in the individual filter-bank outputs, but this aliasing is canceled in the reconstruction by overlap-add if there were no modifications to the STFT. For a general discussion of aliasing cancellation in decimated filter banks, see Chapter 11 (especially §11.4.5) and/or [287].
Next Section:
Filling the FFT Input Buffer (Step 2)
Previous Section:
Further Reading