DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Cyclic FFT Convolution

Thanks to the convolution theorem, we have two alternate ways to perform cyclic convolution in practice:

  1. Direct calculation in the time domain using (8.13)
  2. Frequency-domain convolution:
    1. Fourier Transform both signals
    2. Perform term by term multiplication of the transformed signals
    3. Inverse transform the result to get back to the time domain
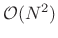
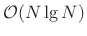
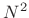
For short convolutions (less than a hundred samples or so), method 1 is usually faster. However, for longer convolutions, method 2 is ultimately faster. This is because the computational complexity of direct cyclic convolution of two $ N$ -point signals is $ {\cal O}(N^2)$ , while that of FFT convolution is $ {\cal O}(N \lg N)$ . 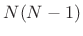More precisely, direct cyclic convolution requires $ N^2$ multiplies and $ N(N-1)$ additions, while the exact FFT numbers depend on the particular FFT algorithm used [80,66,224,277]. Some specific cases are compared in §8.1.4 below.

Next Section:
Acyclic FFT Convolution
Previous Section:
Loudness Spectrogram Examples