DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Acyclic FFT Convolution

If we add enough trailing zeros to the signals being convolved, we can obtain acyclic convolution embedded within a cyclic convolution. How many zeros do we need to add? Suppose the signal $ x(n)$ consists of $ N_x$ contiguous nonzero samples at times 0 to $ N_x-1$ , preceded and followed by zeros, and suppose $ h(n)$ is nonzero only over a block of $ N_h$ samples starting at time 0. Then the acyclic convolution of $ x$ with $ h$ reduces to

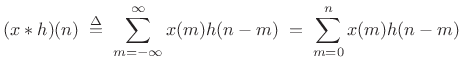$\displaystyle (x\ast h)(n) \isdefs \sum_{m=-\infty}^\infty x(m)h(n-m) \eqsp \sum_{m=0}^n x(m)h(n-m)$ (9.15)

which is zero for $ n<0$ and $ n>(N_x+N_h-1)-1$ . Thus,
$\textstyle \parbox{0.8\textwidth}{\emph{the acyclic convolution of $N_x$\ samples with $N_h$\ samples produces at most $N_x+N_h-1$\ nonzero samples.}}$
The number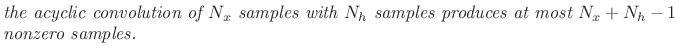 $ N_x+N_h-1$ is easily checked for signals of length 1 since $ \delta\ast \delta = \delta$ , where $ \delta $ is 1 at time zero and 0 at all other times. Similarly,

$\displaystyle [\delta+\hbox{\sc Shift}_1(\delta)] \ast [\delta+\hbox{\sc Shift}_1(\delta)] \eqsp \delta + 2\hbox{\sc Shift}_1(\delta) + \hbox{\sc Shift}_2(\delta)$ (9.16)

and so on.

When $ N_x$ or $ N_h$ is infinity, the convolution result can be as small as 1. For example, consider $ x=[1,r,r^2,r^3,\ldots]$ , with $ \left\vert r\right\vert<1$ , and $ h=[1,-r,0,0,\ldots]$ . Then $ x\ast h = [1, 0, 0, \ldots]$ . This is an example of what is called deconvolution. In the frequency domain, deconvolution always involves a pole-zero cancellation. Therefore, it is only possible when $ N_x$ or $ N_h$ is infinite. In practice, deconvolution can sometimes be accomplished approximately, particularly within narrow frequency bands [119].

We thus conclude that, to embed acyclic convolution within a cyclic convolution (as provided by an FFT), we need to zero-pad both operands out to length $ N$ , where $ N$ is at least the sum of the operand lengths (minus one).

Acyclic Convolution in Matlab

In Matlab or Octave, the conv function implements acyclic convolution: 

octave:1> conv([1 2],[3 4])
ans =
   3  10   8
Note that it returns an output vector which is long enough to accommodate the entire result of the convolution, unlike the filter primitive, which always returns an output signal equal in length to the input signal: 
octave:2> filter([1 2],1,[3 4])
ans =
   3  10
octave:3> filter([1 2],1,[3 4 0])
ans =
   3  10   8

Pictorial View of Acyclic Convolution

Figure 8.2: Schematic depiction of the acyclic convolution of two signals.
\includegraphics[width=\textwidth ]{eps/convwaves}

Figure 8.2 shows schematically the result of convolving two zero-padded signals $ x$ and $ h$ . In this case, the signal $ x(n)$ starts some time after $ n=0$ , say at $ n=n_x$ . Since $ h(n)$ begins at time 0 , the output starts promptly at time $ n_x$ , but it takes some time to ``ramp up'' to full amplitude. (This is the transient response of the FIR filter $ h$ .) If the length of $ h$ is $ N_h$ , then the transient response is finished at time $ n=n_x+N_h-1$ . Next, when the input signal goes to zero at time $ n_x+N_x$ , the output reaches zero $ N_h-1$ samples later (after the filter ``decay time''), or time $ n_x+N_x+N_h-1$ . Thus, the total number of nonzero output samples is $ N_x+N_h-1$ .

If we don't add enough zeros, some of our convolution terms ``wrap around'' and add back upon others (due to modulo indexing). This can be called time-domain aliasing. Zero-padding in the time domain results in more samples (closer spacing) in the frequency domain, i.e., a higher `sampling rate' in the frequency domain. If we have a high enough spectral sampling rate, we can avoid time aliasing.

The motivation for implementing acyclic convolution using a zero-padded cyclic convolution is that we can use a Cooley-Tukey Fast Fourier Transform (FFT) to implement cyclic convolution when its length $ N$ is a power of 2.

Next Section:
Acyclic FFT Convolution in Matlab
Previous Section:
Cyclic FFT Convolution