Free Books
   Free Books    Spectral Audio Signal Processing  

Examples

Figure 4.3 shows the amplitude response of a length $ 30$ optimal least-squares FIR lowpass filter, for the case in which the cut-off frequency is one-fourth the sampling rate ($ f_c=1/4$ ).

Figure: Amplitude response of a length $ 30$ FIR lowpass-filter obtained by truncating the ideal impulse response.
\includegraphics[width=\twidth]{eps/ilpftdlsL30}

We see that, although the impulse response is optimal in the least-squares sense (in fact optimal under any $ Lp$ norm with any error-weighting), the filter is quite poor from an audio perspective. In particular, the stop-band gain, in which zero is desired, is only about 10 dB down. Furthermore, increasing the length of the filter does not help, as evidenced by the length 71 result in Fig.4.4.

Figure: Amplitude response of a length $ 71$ FIR lowpass-filter obtained by truncating the ideal impulse response.
\includegraphics[width=\twidth]{eps/ilpftdlsL71}

It is not the case that a length $ 71$ FIR filter is too short for implementing a reasonable audio lowpass filter, as can be seen in Fig.4.5. The optimal Chebyshev lowpass filter in this figure was designed by the Matlab statement

hh = firpm(L-1,[0 0.5 0.6 1],[1 1 0 0]);
where, in terms of the lowpass design specs defined in §4.2 above, we are asking for
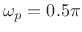  • $ \omega_p = 0.5 \pi$ (pass-band edge frequency)5.5
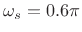  • $ \omega_s = 0.6\pi$ (stop-band edge frequency)
In this case, the pass-band and stop-band ripple are equally weighted and thus are minimized equally for the given FIR length $ L$ .5.6

Figure: Amplitude response of a length $ 71$ FIR lowpass-filter obtained by the Remez Exchange Algorithm (function firpm in the Matlab Signal Processing Toolbox).
\includegraphics[width=\twidth]{eps/ilpfchebL71}

We see that the Chebyshev design has a stop-band attenuation better than 60 dB, no corner-frequency resonance, and the error is equiripple in both stop-band (visible) and pass-band (not visible). Note also that there is a transition band between the pass-band and stop-band (specified in the call to firpm as being between normalized frequencies 0.5 and 0.6).

The main problem with the least-squares design examples above is the absence of a transition band specification. That is, the filter specification calls for an infinite roll-off rate from the pass-band to the stop-band, and this cannot be accomplished by any FIR filter. (Review Fig.4.2 for an illustration of more practical lowpass-filter design specifications.) With a transition band and a weighting function, least-squares FIR filter design can perform very well in practice. As a rule of thumb, the transition bandwidth should be at least $ 4\pi/L$ , where $ L$ is the FIR filter length in samples. (Recall that the main-lobe width of a length $ L$ rectangular window is $ 4\pi/L$ (§3.1.2).) Such a rule respects the basic Fourier duality of length in the time domain and ``minimum feature width'' in the frequency domain.

Next Section:
Matlab Support for the Window Method
Previous Section:
Ideal Lowpass Filter Revisited