DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Rectangular Window Summary

The rectangular window was discussed in Chapter 5 (§3.1). Here we summarize the results of that discussion.

Definition ($ M$ odd):

$\displaystyle w_R(n) \isdef \left\{\begin{array}{ll} 1, & \left\vert n\right\vert\leq\frac{M-1}{2} \\ [5pt] 0, & \hbox{otherwise} \\ \end{array} \right.$ (4.12)

Transform:

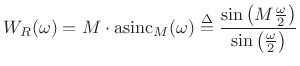$\displaystyle W_R(\omega) = M\cdot \hbox{asinc}_M(\omega) \isdef \frac{\sin\left(M\frac{\omega}{2}\right)}{\sin\left(\frac{\omega}{2}\right)}$ (4.13)

The DTFT of a rectangular window is shown in Fig.3.7.

Figure 3.7: Rectangular window discrete-time Fourier transform.
\includegraphics[width=\twidth]{eps/Rect}

Properties:

  • Zero crossings at integer multiples of

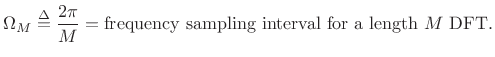
    $\displaystyle \Omega_M \isdef \frac{2\pi}{M} = \hbox{frequency sampling interval for a length $M$\ DFT.}$ (4.14)

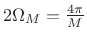  • Main lobe width is $ 2 \Omega_M = \frac{4\pi}{M} $ .
  • As $ M$ increases, the main lobe narrows (better frequency resolution).
  • $ M$ has no effect on the height of the side lobes (same as the ``Gibbs phenomenon'' for truncated Fourier series expansions).
  • First side lobe only 13 dB down from the main-lobe peak.
  • Side lobes roll off at approximately 6dB per octave.
  • A phase term arises when we shift the window to make it causal, while the window transform is real in the zero-phase case (i.e., centered about time 0).

Next Section:
Hann or Hanning or Raised Cosine
Previous Section:
Rectangular Window Side-Lobes