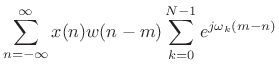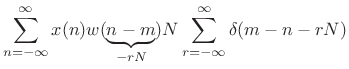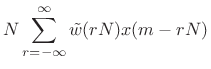FBS Window Constraints for R=1
Recall that in overlap-add (Chapter 8), perfect
reconstruction required only that the analysis window ![]() meet a
constant overlap-add (COLA) constraint:
meet a
constant overlap-add (COLA) constraint:
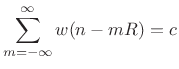 |
(10.18) |
where
The Filter Bank Summation (FBS) is interpreted as a demodulation
(frequency shift by ![]() ) and subsequent lowpass filtering by
) and subsequent lowpass filtering by
![]() . Therefore, to
resynthesize our original signal, we need to remodulate each
baseband signal and sum up the channels. For
. Therefore, to
resynthesize our original signal, we need to remodulate each
baseband signal and sum up the channels. For ![]() (no
downsampling), this sum is given by [9]
(no
downsampling), this sum is given by [9]
We have thus derived the following sufficient condition for perfect reconstruction [213]:
Since normally our windows are shorter than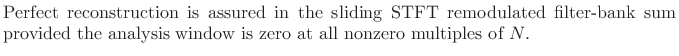
Next Section:
Nyquist(N) Windows
Previous Section:
The DFT Filter Bank








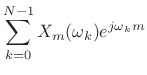
![$\displaystyle \sum_{k=0}^{N-1} \left[ \sum_{n=-\infty}^\infty
x(n)w(n-m)e^{-j\omega_kn} \right] e^{j\omega_km}$](http://www.dsprelated.com/josimages_new/sasp2/img1614.png)