DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Filter Banks Equivalent to STFTs

We now turn to various practical examples of perfect reconstruction filter banks, with emphasis on those using FFTs in their implementation (i.e., various STFT filter banks).

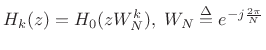Figure 11.28 illustrates a generic filter bank with $ N=3$ channels, much like we derived in §9.3. The analysis filters $ H_{k}(z)$ , $ k=1, \ldots, N$ are bandpass filters derived from a lowpass prototype $ H_{0}(z)$ by modulation (e.g., $ H_{k}(z) = H_{0}(zW_N^k),\; W_N \isdef e^{-j\frac{2 \pi}{N}}$ ), as shown in the right portion of the figure. The channel signals $ X_n(\omega_k)$ are given by the convolution of the input signal with the $ k$ th channel impulse response:

$\displaystyle X_n(\omega_k) \eqsp \sum_{m=-\infty}^{\infty} x(m) h_{0}(n-m)W_N^{-km} \protect$ (12.95)

From Chapter 9, we recognize this expression as the sliding-window STFT, where $ h_{0}(n-m)$ is the flip of a sliding window ``centered'' at time $ n$ , and $ X_{n}(\omega_k)$ is the $ k$ th DFT bin at time $ n$ . We also know from that discussion that remodulating the DFT channel outputs and summing gives perfect reconstruction of $ x(n)$ whenever $ h_{0}(n)$ is Nyquist(N) (the defining condition for Portnoff windows [213], §9.7).

\begin{psfrags} % latex2html id marker 30457\psfrag{z^-1}{{\large $z^{-1}$}}\psfrag{X(z)}{{\large $X(z)$}}\psfrag{X0(z)}{{\large $X_0(z)$}}\psfrag{X1(z)}{{\large $X_1(z)$}}\psfrag{X2(z)}{{\large $X_2(z)$}}\psfrag{Xn[0]}{{\normalsize $X_n(\omega_0)$}}\psfrag{Xn[1]}{{\normalsize $X_n(\omega_1)$}}\psfrag{Xn[2]}{{\normalsize $X_n(\omega_2)$}}\psfrag{H0(z)}{{\large $H_0(z)$}}\psfrag{H1(z)}{{\large $H_1(z)$}}\psfrag{H2(z)}{{\large $H_2(z)$}}\psfrag{W(-0n,N)}{{\small $W_N^{0n}$}}\psfrag{W(-1n,N)}{{\small $W_N^{-1n}$}}\psfrag{W(-2n,N)}{{\small $W_N^{-2n}$}}\psfrag{W(0n,N)}{{\small $W_N^{0n}$}}\psfrag{W(1n,N)}{{\small $W_N^{1n}$}}\psfrag{W(2n,N)}{{\small $W_N^{2n}$}}\psfrag{STFT}{}\begin{figure}[htbp] \includegraphics[width=\twidth]{eps/portnoff} \caption{Portnoff analysis bank for $N=3$.} \end{figure} \end{psfrags}

Suppose the analysis window $ w$ (flip of the baseband-filter impulse response $ h_0$ ) is length $ L>N$ . Then in the context of overlap-add processors (Chapter 8), $ w$ is a Portnoff window, and implementing the window with a length $ N$ FFT requires that the windowed data frame be time-aliased down to length $ N$ prior to taking a length $ N$ FFT (see §9.7). We can obtain this same result via polyphase analysis, as elaborated in the next section.

Polyphase Analysis of Portnoff STFT

Consider the $ k$ th filter-bank channel filter

$\displaystyle H_{k}(z) \eqsp H_{0}(zW_N^k), \; k=1,\ldots,N-1\,.$ (12.96)

The impulse-response $ h_0(n)$ can be any length $ L$ sequence. Denote the $ N$ -channel polyphase components of $ H_0(z)$ by $ E_l(z)$ , $ l=0,1,\ldots,N-1$ . Then by the polyphase decomposition (§11.2.2), we have

\begin{eqnarray*} H_{0}(z) & = & \sum_{l=0}^{N-1} z^{-l}E_l(z^{N}) \\ [5pt] H_{k}(z) & = & \sum_{l=0}^{N-1} (zW_N^k)^{-l} E_l[(z W_N^k)^{N}] \\ [5pt] & = & \sum_{l=0}^{N-1} z^{-l} E_l(z^{N}) W_N^{-kl}. \end{eqnarray*}

Consequently,

\begin{eqnarray*} H_{k}(z)X(z) & = & \sum_{l=0}^{N-1} z^{-l} E_l(z^{N})X(z) W_N^{-kl} \\ \left[\begin{array}{c} H_{0}(z) \\ \ldots \\ H_{N-1}(z) \end{array} \right] & = & \left[\begin{array}{ccc} & & \\ & W_N^{-kl} & \\ & & \end{array} \right] \left[\begin{array}{c} E_0(z^N) z^{-0} X(z) \\ \ldots \\ E_{N-1}(z^N) z^{-(N-1)} X(z) \end{array} \right]. \end{eqnarray*}

If $ H_{0}(z)$ is a good $ N$ th-band lowpass, the subband signals $ x_{k}(n)$ are bandlimited to a region of width $ 2\pi/N$ . As a result, there is negligible aliasing when we downsample each of the subbands by $ N$ . Commuting the downsamplers to get an efficient implementation gives Fig.11.29.

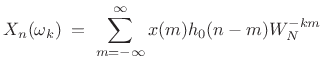
\begin{psfrags} % latex2html id marker 30545\psfrag{X(z)}{{\large $X(z)$}}\psfrag{E0(z^3)}{{\large $E_0(z^3)$}}\psfrag{E1(z^3)}{{\large $E_1(z^3)$}}\psfrag{E2(z^3)}{{\large $E_2(z^3)$}}\psfrag{E0(z)}{{\large $E_0(z)$}}\psfrag{E1(z)}{{\large $E_1(z)$}}\psfrag{E2(z)}{{\large $E_2(z)$}}\psfrag{X0(z)}{{\large $X_0(z)$}}\psfrag{X1(z)}{{\large $X_1(z)$}}\psfrag{X2(z)}{{\large $X_2(z)$}}\begin{figure}[htbp] \includegraphics[width=\twidth]{eps/polystft} \caption{Polyphase implementation of Portnoff STFT filter bank for $N=3$.} \end{figure} \end{psfrags}

First note that if $ E_k(z) = 1$ for all $ k$ , the system of Fig.11.29 reduces to a rectangularly windowed STFT in which the window length $ M$ equals the DFT length $ N=3$ . The downsamplers ``hold off'' the DFT until the length 3 delay line fills with new input samples, then it ``fires'' to produce a spectral frame. A new spectral frame is produced after every third sample of input data is received.

In the more general case in which $ E_k(z)$ are nontrivial filters, such as $ E_k(z)=1+z^{-1}$ , for example, they can be seen to compute the equivalent of a time aliased windowed input frame, such as $ x(n) + x(n-N)$ . This follows because the filters operate on the downsampled input stream, so that the filter coefficients operate on signal samples separated by $ N$ samples. The linear combination of these samples by the filter implements the time-aliased windowed data frame in a Portnoff-windowed overlap-add STFT. Taken together, the polyphase filters $ E_k(z)$ compute the appropriately time-aliased data frame windowed by $ w=\hbox{\sc Flip}(h_0)\;\leftrightarrow\;H_{0}(z^{-1})$ .

In the overlap-add interpretation of Fig.11.29, the window is hopped by $ N=3$ samples. While this was the entire window length in the rectangular window case ($ E_k(z) = 1$ ), it is only a portion of the effective frame length $ L$ when the analysis filters have order 1 or greater.

Next Section:
MPEG Filter Banks
Previous Section:
Paraunitary Filter Banks