DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

MPEG Filter Banks

This section provides some highlights of the history of filter banks used for perceptual audio coding (MPEG audio). For a more complete introduction and discussion of MPEG filter banks, see, e.g., [16,273].

Pseudo-QMF Cosine Modulation Filter Bank

Section 11.3.5 introduced two-channel quadrature mirror filter banks (QMF). QMFs were shown to provide a particular class of perfect reconstruction filter banks. We found, however, that the quadrature mirror constraint on the analysis filters,

$\displaystyle H_1(z) \eqsp H_0(-z),$ (12.97)

was rather severe in that linear-phase FIR implementations only exist in the two-tap case $ H_k(z) = h_{0k}+h_{1k}z^{-1}$ , $ k=0,1$ . In addition to relaxing this constraint, we need to be able to design an $ N$ -channel filter bank for any $ N$ .

The Pseudo-QMF (PQMF) filter bank is a ``near perfect reconstruction'' filter bank in which aliasing cancellation occurs only between adjacent bands [194,287]. The PQMF filters commonly used in perceptual audio coders employ bandpass filters with stop-band attenuation near $ 96$ dB, so the neglected bands (which alias freely) are not significant. An outline of the design procedure is as follows:

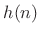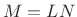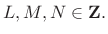
  1. Design a lowpass prototype window, $ h(n)$ , with length $ M=LN$ , $ L,M,N \in {\bf Z}.$
  2. The lowpass design is constrained to give aliasing cancellation in neighboring subbands:

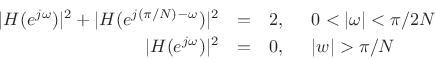
    \begin{eqnarray*} \vert H(e^{j\omega})\vert^2 + \vert H(e^{j(\pi/N)-\omega})\vert^2 &=& 2, \hspace{.5cm}0 < \vert\omega\vert < \pi/{2N} \\ \vert H(e^{j\omega})\vert^2 &=& 0, \hspace{.5cm}\vert w\vert > \pi/N \end{eqnarray*}

  3. The filter bank analysis filters 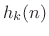$ h_k(n)$ are cosine modulations of $ h(n)$ :

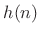    $\displaystyle h_k(n) \eqsp h(n)\hbox{cos}\left[\left(k+\frac{1}{2}\right)\left(n-\frac{M-1}{2}\right)\frac{\pi}{N} + \phi_k\right],$ (12.98)

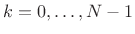    $ k=0,\ldots,N-1$ , where the phases are restricted according to

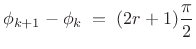
    $\displaystyle \phi_{k+1} - \phi_k \eqsp (2r+1)\frac{\pi}{2}$ (12.99)

    again for aliasing cancellation.
  4. Since it is an orthogonal filter bank by construction, the synthesis filters are simply the time-reverse of the analysis filters:

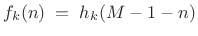
    $\displaystyle f_k(n) \eqsp h_k(M-1-n)$ (12.100)

This PQMF filter bank is reportedly used in MPEG audio, layers I and II with $ N=32$ bands and $ M=512$ taps ($ L=8$ ).

Perfect Reconstruction Cosine Modulated Filter Banks

By changing the phases $ \phi_k$ , the pseudo-QMF filter bank can yield perfect reconstruction:

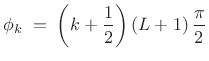$\displaystyle \phi_k \eqsp \left(k+\frac{1}{2}\right)\left(L+1\right)\frac{\pi}{2}$ (12.101)

where $ L$ is the length of the polyphase filter ($ M=LN$ ).

If $ M=2N$ , then this is the oddly stacked Princen-Bradley filter bank and the analysis filters are related by cosine modulations of the lowpass prototype:

$\displaystyle f_k(n) \eqsp h(n)\hbox{cos}\left[\left(n+\frac{N+1}{2}\right)\left(k+\frac{1}{2}\right)\frac{\pi}{N}\right],\quad k=0,\ldots,N-1$ (12.102)

However, the length of the filters $ M$ can be any even multiple of $ N$ :

$\displaystyle M\eqsp LN, \quad (L/2) \in \cal{Z}$ (12.103)

The parameter $ L$ is called the overlapping factor. These filter banks are also referred to as extended lapped transforms, when $ K \ge 2$ [159].

MPEG Layer III Filter Bank

MPEG 1 and 2, Layer III is popularly known as ``MP3 format.'' The original MPEG 1 and 2, Layers I and II, based on the MUSICAM coder, contained only 32 subbands, each band approximately 650 Hz wide, implemented using a length 512 lowpass-prototype window, lapped (``time aliased'') by factor of 512/32 = 16, thus yielding 32 real bands with 96 dB of stop-band rejection, and having a hop size of 32 samples [149, §4.1.1]. It was found, however, that a higher coding gain was obtained using a finer frequency resolution. As a result, the MPEG 1&2 Layer III coder (based on the ASPEC coder from AT&T), appended a Princen-Bradley filter bank [214] having 6 to 18 subbands to the output of each subband of the 32-channel PQMF cosine-modulated analysis filter bank [149, § 4.1.2]. The number of sub-bands and window shape were chosen to be signal-dependent as follows:

  • Transients use 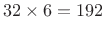$ 32\times 6=192$ subbands, corresponding to relatively high time resolution and low frequency resolution.
  • Steady-state tones use 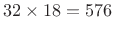$ 32\times 18=576$ subbands, corresponding to higher frequency resolution and lower time resolution relative to transients.12.3
  • The encoder generates a function called the perceptual entropy (PE) which tells the coder when to switch resolutions.

The MPEG AAC coder is often regarded as providing nearly twice the compression ratio of ``MP3'' (MPEG 1-2 Layer III) coding at the same quality level.12.4 MPEG AAC introduced a new MDCT filter bank that adaptively switches between 128 and 1024 bands (length 256 and 2048 FFT windows, using 50% overlap) [149, §4.1.6]. The nearly doubled number of frequency bands available for coding steady-state signal intervals contributed much to the increased coding gain of AAC over MP3. The 128-1024 MDCT filter bank in AAC is also considerably simpler than the hierarchical $ 32\times 6$ -$ 18$ MP3 filter bank, without requiring the ``cross-talk aliasing reduction'' needed by the PQMF/MDCT hierarchical filter bank of MP3 [149, §4.1.6].

The MPEG-4 audio compression standard (there was no MPEG-3), included a new transform coder based on the AAC filter bank [149, §4.1.7].

See, e.g., [16,273] for much more on MPEG coders and related topics. Chapter 4 of [149] contains an excellent summary of MPEG, Sony ATRAC, and Dolby AC-n coders up to 1998.

Next Section:
Review of STFT Filterbanks
Previous Section:
Filter Banks Equivalent to STFTs