DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Filter Design Example

Figure: Filter Design Example: Overlay of measured and modeled magnitude transfer functions, where the model is a $ 12$ th-order filter designed by Prony's method. a) Results without prewarping of the frequency axis. b) Results using the Bark bilinear transform prewarping.
\includegraphics[width=\twidth]{eps/fd}

We conclude discussion of the Bark bilinear transform with the filter design example of Fig.E.9. A $ 12$ th-order pole-zero filter was fit using Prony's method [162] to the equalization function plotted in the figure as a dashed line. Prony's method was applied normally over a uniformly sampled linear frequency grid in the example of Fig.E.9a, and over an approximate Bark-scale axis in the example of Fig.E.9b. The procedure in the Bark-scale case was as follows [258]:E.2

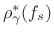  1. The optimal allpass coefficient $ \rho ^*_{\mathbf\gamma}(f_s)$ was found using (E.3.5).

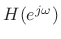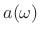  2. The desired frequency response $ H(e^{j\omega})$ defined on a linear frequency axis $ \omega$ was warped to an approximate Bark scale $ a(\omega )$ using the Bark bilinear transform, $ {\tilde H}(e^{j\omega }) \isdef H[{\cal A}_{\rho }(e^{ja(\omega )})]$ .

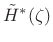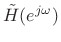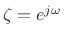  3. A parametric ARMA model $ {\tilde H}^*(\zeta )$ was fit to the desired Bark-warped frequency response $ {\tilde H}(e^{j\omega })$ over the unit circle $ \zeta =e^{j\omega }$ .

  4. Finally, the inverse Bark bilinear transform 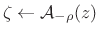$ \zeta \leftarrow {\cal A}_{-\rho }(z)$ was used to ``unwarp'' the modeled system to a linear frequency axis.

Referring to Fig.E.9, it is clear that the warped solution provides a better overall fit than the direct solution which sacrifices accuracy below $ 4$  kHz to achieve a tighter fit above $ 10$  kHz. In some part, the spacing of spectral features is responsible for the success of the Bark-warped model in this particular example. However, we generally recommend using the Bark bilinear transform to design audio filters, since doing so weights the error norm (for norms other than Chebyshev types) in a way which gives equal importance to matching features having equal Bark bandwidths. Even in the case of Chebyshev optimization, auditory warping appears to improve the numerical conditioning of the filter design problem; this applies also to optimization under the Hankel norm which includes an optimal Chebyshev design internally as an intermediate step. Further filter-design examples, including more on the Hankel-norm case, may be found in [258].

Next Section:
ERB Relative Bandwidth Mapping Error
Previous Section:
Arctangent Approximations for