Gaussian Windowed Chirps (Chirplets)

Free Books Spectral Audio Signal Processing

As discussed in §G.8.2, an interesting generalization of sinusoidal modeling is chirplet modeling. A chirplet is defined as a Gaussian-windowed sinusoid, where the sinusoid has a constant amplitude, but its frequency may be linearly ``sweeping.'' This definition arises naturally from the mathematical fact that the Fourier transform of a Gaussian-windowed chirp signal is a complex Gaussian pulse, where a chirp signal is defined as a sinusoid having linearly modulated frequency, i.e., quadratic phase:

$\displaystyle s(t) \eqsp e^{j\beta t^2}$

(11.25)

Applying a Gaussian window to this chirp yields

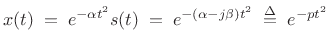$\displaystyle x(t) \eqsp e^{-\alpha t^2} s(t) \eqsp e^{-(\alpha-j\beta) t^2} \isdefs e^{-p t^2}$

(11.26)

where 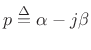$p\isdef \alpha-j\beta$ . It is thus clear how naturally Gaussian amplitude envelopes and linearly frequency-sweeping sinusoids (chirps) belong together in a unified form called a chirplet.

The basic chirplet $x(t)=e^{-p t^2}$ can be regarded as an exponential polynomial signal in which the polynomial is of order 2. Exponential polynomials of higher order have also been explored [89,90,91]. (See also §G.8.2.)

Chirplet Fourier Transform

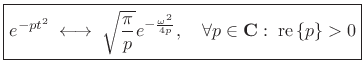
The Fourier transform of a complex Gaussian pulse is derived in §D.8 of Appendix D:

$\displaystyle \zbox {e^{-pt^2} \;\longleftrightarrow\;\sqrt{\frac{\pi}{p}} e^{-\frac{\omega^2}{4p}},\quad \forall p\in {\bf C}: \; \mbox{re}\left\{p\right\}>0} \protect$

(11.27)

This result is valid when is complex. Writing in terms of real variables $\alpha$ and $\beta$ as

$\displaystyle p \eqsp \alpha - j\beta,$

(11.28)

we have

$\displaystyle x(t) \eqsp e^{-p t^2} \eqsp e^{-\alpha t^2} e^{j\beta t^2} \eqsp e^{-\alpha t^2} \left[\cos(\beta t^2) + j\sin(\beta t^2)\right].$

(11.29)

That is, for complex, is a chirplet (Gaussian-windowed chirp). We see that the chirp oscillation frequency is zero at time . Therefore, for signal modeling applications, we typically add in an arbitrary frequency offset at time 0, as described in the next section.

Modulated Gaussian-Windowed Chirp

By the modulation theorem for Fourier transforms,

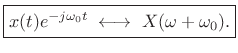$\displaystyle \zbox {x(t)e^{-j\omega_0t}\;\longleftrightarrow\;X(\omega+\omega_0).}$

(11.30)

This is proved in §B.6 as the dual of the shift-theorem. It is also evident from inspection of the Fourier transform:

$\displaystyle \int_{-\infty}^\infty \left[x(t)e^{-j\omega_0 t}\right] e^{-j\omega t} dt \eqsp \int_{-\infty}^\infty x(t)e^{-j(\omega+\omega_0) t} dt \isdefs X(\omega+\omega_0)$

(11.31)

Applying the modulation theorem to the Gaussian transform pair above yields

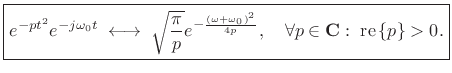$\displaystyle \zbox {e^{-pt^2} e^{-j\omega_0 t} \;\longleftrightarrow\;\sqrt{\frac{\pi}{p}} e^{-\frac{(\omega+\omega_0)^2}{4p}},\quad \forall p\in {\bf C}: \; \mbox{re}\left\{p\right\}>0.}$

(11.32)

Thus, we frequency-shift a Gaussian chirp in the same way we frequency-shift any signal--by complex modulation (multiplication by a complex sinusoid at the shift-frequency).

Identifying Chirp Rate

Consider again the Fourier transform of a complex Gaussian in (10.27):

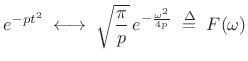$\displaystyle e^{-pt^2} \;\longleftrightarrow\;\sqrt{\frac{\pi}{p}} \, e^{-\frac{\omega^2}{4p}}\;\isdef \;F(\omega)$

(11.33)

Setting $p=\alpha - j\beta$ gives

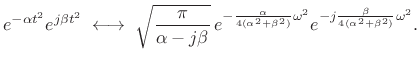$\displaystyle e^{-\alpha t^2} e^{j\beta t^2} \;\longleftrightarrow\; \sqrt{\frac{\pi}{\alpha-j\beta}} \, e^{-\frac{\alpha}{4(\alpha^2+\beta^2)}\omega^2} e^{-j\frac{\beta}{4(\alpha^2+\beta^2)}\omega^2}.$

(11.34)

The log magnitude Fourier transform is given by

$\displaystyle \ln\left\vert F(\omega)\right\vert \eqsp \hbox{constant} -\frac{\alpha}{4(\alpha^2+\beta^2)}\omega^2$

(11.35)

and the phase is

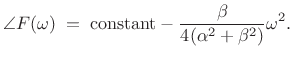$\displaystyle \angle F(\omega) \eqsp \hbox{constant} -\frac{\beta}{4(\alpha^2+\beta^2)}\omega^2.$

(11.36)

Note that both log-magnitude and (unwrapped) phase are parabolas in $\omega$ .

In practice, it is simple to estimate the curvature at a spectral peak using parabolic interpolation:

$\begin{eqnarray*} c_m &\isdef & \frac{d^2}{d\omega^2} \ln\vert F(\omega)\vert \eqsp - \frac{\alpha}{2(\alpha^2+\beta^2)}\\ [5pt] c_p &\isdef & \frac{d^2}{d\omega^2} \angle F(\omega) \eqsp - \frac{\beta}{2(\alpha^2+\beta^2)} \end{eqnarray*}$

We can write

$\begin{eqnarray*} \zbox {\frac{d^2}{d\omega^2} \ln F(\omega) \eqsp c_m + jc_p \eqsp - \frac{\alpha}{2(\alpha^2+\beta^2)} - j\frac{\beta}{2(\alpha^2+\beta^2)}.} \end{eqnarray*}$

Note that the window ``amplitude-rate'' $\alpha$ is always positive. The ``chirp rate'' $\beta$ may be positive (increasing frequency) or negative (downgoing chirps). For purposes of chirp-rate estimation, there is no need to find the true spectral peak because the curvature is the same for all $\omega$ . However, curvature estimates are generally more reliable near spectral peaks, where the signal-to-noise ratio is typically maximum. In practice, we can form an estimate of $\alpha$ from the known FFT analysis window (typically ``close to Gaussian'').

Chirplet Frequency-Rate Estimation

The chirp rate $\beta$ may be estimated from the relation $\beta = \alpha c_m/c_p$ as follows:

Let 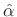${\hat \alpha}$ denote the measured (or known) curvature at the midpoint of the analysis window .
Let and denote weighted averages of the measured curvatures 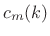and 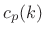along the log-magnitude and phase of a spectral peak, respectively.
Then the chirp-rate $\beta$ estimate may be estimated from the spectral peak by

$\displaystyle \zbox {{\hat \beta}\isdefs {\hat \alpha}\frac{[c_p]}{[c_m]}}$

Simulation Results

**Figure 10.24:** Real Gaussian-windowed chirp (time domain).
$\includegraphics[width=\twidth]{eps/gwchirp}$

Figure 10.24 shows the waveform of a Gaussian-windowed chirp (``chirplet'') generated by the following matlab code:

fs = 8000;
x = chirp([0:1/fs:0.1],1000,1,2000);
M = length(x);
n=(-(M-1)/2:(M-1)/2)';
w = exp(-n.*n./(2*sigma.*sigma));
xw = w(:) .* x(:);

Figure 10.25 shows the same chirplet in a time-frequency plot. Figure 10.26 shows the spectrum of the example chirplet. Note the parabolic fits to dB magnitude and unwrapped phase. We see that phase modeling is most accurate where magnitude is substantial. If the signal were not truncated in the time domain, the parabolic fits would be perfect. Figure 10.27 shows the spectrum of a Gaussian-windowed chirp in which frequency decreases from 1 kHz to 500 Hz. Note how the curvature of the phase at the peak has changed sign.

**Figure 10.25:** Real Gaussian-windowed chirp (spectrogram).
$\includegraphics[width=\twidth]{eps/gwchirpsgC}$

**Figure 10.26:** Gaussian-windowed chirp (frequency domain).
$\includegraphics[width=\twidth]{eps/gwchirpxform}$

**Figure 10.27:** Downgoing chirp.
$\includegraphics[width=\twidth]{eps/gwchirpdownxform}$

**Figure 10.28:** Short chirp--time waveform.
$\includegraphics[width=\twidth,height=3in]{eps/gwchirpshort}$

**Figure 10.29:** Short chirp--spectrum.
$\includegraphics[width=\twidth]{eps/gwchirpshortxform}$

Next Section:
FFT Filter Banks
Previous Section:
Time Scale Modification