Free Books    Spectral Audio Signal Processing  

Frequency Resolution

The frequency resolution of a spectrum-analysis window is determined by its main-lobe width (Chapter 3) in the frequency domain, where a typical main lobe is illustrated in Fig.5.6 (top). For maximum frequency resolution, we desire the narrowest possible main-lobe width, which calls for the rectangular window (§3.1), the transform of which is shown in Fig.3.3. When we cannot be fooled by the large side-lobes of the rectangular window transform (e.g., when the sinusoids under analysis are known to be well separated in frequency), the rectangular window truly is the optimal window for the estimation of frequency, amplitude, and phase of a sinusoid in the presence of stationary noise [230,120,121].

The rectangular window has only one parameter (aside from amplitude)--its length. The next section looks at the effect of an increased window length on our ability to resolve two sinusoids.

Two Cosines (``In-Phase'' Case)

Figure 5.7 shows a spectrum analysis of two cosines

$\displaystyle x(n) = \cos(\omega_1 n) + \cos(\omega_2 n), \quad n=0,1,\ldots,M-1,$ (6.17)

where $ \omega_1 = \pi/2$ and $ \omega_2 = \omega_1 + \Delta\omega$ , and the frequency separation $ \Delta \omega = \omega_2-\omega_1$ is $ 2\pi/40$ radians per sample. The zero-padded Fourier analysis uses rectangular windows of lengths $ M=20$ , $ 30$ , $ 40$ , and $ 80$ ( $ \Delta\omega = \frac{1}{2}\Omega_M, \frac{3}{4}\Omega_M, \Omega_M, 2\Omega_M$ , where $ \Omega_M\isdef 2\pi/M$ ). The length $ N=1024$ FFT output is divided by $ M$ so that the ideal height of each spectral peak is $ \max_{\omega_k}\{\vert X(\omega_k)\vert\}=1/2$ .

Figure: DTFT of two closely spaced in-phase sinusoids, various rectangular-window lengths $ M$ .
\includegraphics[width=\twidth]{eps/resolvedSines}

The longest window ($ M=80$ ) resolves the sinusoids very well, while the shortest case ($ M=20$ ) does not resolve them at all (only one ``lump'' appears in the spectrum analysis). In difference-frequency cycles, the analysis windows are two cycles and half a cycle in these cases, respectively. It can be debated whether or not the other two cases are resolved, and we will return to them shortly.

One Sine and One Cosine ``Phase Quadrature'' Case

Figure 5.8 shows a similar spectrum analysis of two sinusoids

$\displaystyle x(n) = \sin(\omega_1 n) + \cos(\omega_2 n), \quad n=0,1,\ldots,M-1,$ (6.18)

using the same frequency separation and window lengths. However, now the sinusoids are 90 degrees out of phase (one sine and one cosine). Curiously, the top-left case ( $ M=20=\hbox{1/2 difference-frequency cycle}$ ) now appears to be resolved! However, closer inspection (see Fig.5.9) reveals that the ``resolved'' spectral peaks are significantly far away from the sinusoidal frequencies. Another curious observation is that the lower-left case ( $ M=40=\hbox{1 difference-frequency cycle}$ ) appears worse off than it did in Fig.5.7, and worse than the shorter-window analysis at the top right of Fig.5.8. Only the well resolved case at the lower right (spanning two full cycles of the difference frequency) appears unaffected by the relative phase of the two sinusoids under analysis.

Figure: DTFT of two closely spaced sinusoids in phase quadrature, various window lengths $ M$ .
\includegraphics[width=\twidth]{eps/resolvedSinesB}

Figure 5.9 shows the same plots as in Fig.5.8, but overlaid. From this we can see that the peak locations are biased in under-resolved cases, both in amplitude and frequency.

Figure: Overlay of the plots in Fig.5.8.
\includegraphics[width=\textwidth ]{eps/resolvedSinesC2C}

The preceding figures suggest that, for a rectangular window of length $ M$ , two sinusoids are well resolved when they are separated in frequency by

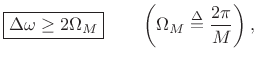$\displaystyle \zbox {\Delta\omega\geq 2\Omega_M} \qquad \left(\Omega_M \isdef \frac{2\pi}{M}\right),$ (6.19)

where the frequency-separation $ \Delta \omega = \omega_2-\omega_1$ is in radians per sample. In cycles per sample, the inequality becomes

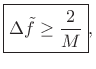$\displaystyle \zbox {\Delta {\tilde f}\geq \frac{2}{M}},$ (6.20)

where the 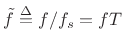$ {\tilde f}\isdef f/f_s = fT$ denotes normalized frequency in cycles per sample. In Hz, we have

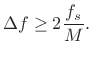$\displaystyle \Delta f\geq 2\frac{f_s}{M}.$ (6.21)

or

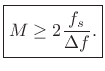$\displaystyle \zbox {M \geq 2\frac{f_s}{\Delta f}.}$ (6.22)

Note that $ f_s/f$ is the number of samples in one period of a sinusoid at frequency $ f$ Hz, sampled at $ f_s$ Hz. Therefore, we have derived a rule of thumb for frequency resolution that requires at least two full cycles of the difference-frequency under the rectangular window.

A more detailed study [1] reveals that $ 1.44$ cycles of the difference-frequency is sufficient to enable fully accurate peak-frequency measurement under the rectangular window by means of finding FFT peaks. In §5.5.2 below, additional minimum duration specifications for resolving closely spaced sinusoids are given for other window types as well.

In principle, we can resolve arbitrarily small frequency separations, provided

  • there is no noise, and
  • we are sure we are looking at the sum of two ideal sinusoids under the window.
One method for doing this is described in §5.7.2. However, in practice, there is almost always some noise and/or interference from other signals, so we normally prefer to require sinusoidal frequency separation by on the order of one main-lobe width or more.

The rectangular window provides an abrupt transition at its edge. While it remains the optimal window for sinusoidal peak estimation, it is by no means optimal in all spectrum analysis and/or signal processing applications involving spectral processing. As discussed in Chapter 3, windows with a more gradual transition to zero have lower side-lobe levels, and this is beneficial for spectral displays and various signal processing applications based on FFT methods. We will encounter such applications in later chapters.

Next Section:
Other Definitions of Main Lobe Width
Previous Section:
Nonlinear Optimization in Matlab