Free Books
   Free Books    Spectral Audio Signal Processing  

White Noise


Definition: To say that $ v(n)$ is a white noise means merely that successive samples are uncorrelated:

$\displaystyle E\{v(n)v(n+m)\} = \left\{\begin{array}{ll} \sigma_v^2, & m=0 \\ [5pt] 0, & m\neq 0 \\ \end{array} \right. \isdef \sigma_v^2 \delta(m) \protect$ (C.26)

where $ E\{f(v)\}$ denotes the expected value of $ f(v)$ (a function of the random variables $ v(n)$ ).

In other words, the autocorrelation function of white noise is an impulse at lag 0. Since the power spectral density is the Fourier transform of the autocorrelation function, the PSD of white noise is a constant. Therefore, all frequency components are equally present--hence the name ``white'' in analogy with white light (which consists of all colors in equal amounts).

Making White Noise with Dice

An example of a digital white noise generator is the sum of a pair of dice minus 7. We must subtract 7 from the sum to make it zero mean. (A nonzero mean can be regarded as a deterministic component at dc, and is thus excluded from any pure noise signal for our purposes.) For each roll of the dice, a number between $ 1+1-7 = -5$ and $ 6+6-7=5$ is generated. The numbers are distributed binomially between $ -5$ and $ 5$ , but this has nothing to do with the whiteness of the number sequence generated by successive rolls of the dice. The value of a single die minus $ 3.5$ would also generate a white noise sequence, this time between $ -2.5$ and $ +2.5$ and distributed with equal probability over the six numbers

$\displaystyle \left[-\frac{5}{2}, -\frac{3}{2}, -\frac{1}{2}, \frac{1}{2}, \frac{3}{2}, \frac{5}{2}\right].$ (C.27)

To obtain a white noise sequence, all that matters is that the dice are sufficiently well shaken between rolls so that successive rolls produce independent random numbers.C.4

Independent Implies Uncorrelated

It can be shown that independent zero-mean random numbers are also uncorrelated, since, referring to (C.26),

$\displaystyle E\{\overline{v(n)}v(n+m)\} = \left\{\begin{array}{ll} E\{\left\vert v(n)\right\vert^2\} = \sigma_v^2, & m=0 \\ [5pt] E\{\overline{v(n)}\}\cdot E\{v(n+m)\}=0, & m\neq 0 \\ \end{array} \right. \isdef \sigma_v^2 \delta(m)$ (C.28)

For Gaussian distributed random numbers, being uncorrelated also implies independence [201]. For related discussion illustrations, see §6.3.

Estimator Variance

As mentioned in §6.12, the pwelch function in Matlab and Octave offer ``confidence intervals'' for an estimated power spectral density (PSD). A confidence interval encloses the true value with probability $ P$ (the confidence level). For example, if $ P=0.99$ , then the confidence level is $ 99\%$ .

This section gives a first discussion of ``estimator variance,'' particularly the variance of sample means and sample variances for stationary stochastic processes.

Sample-Mean Variance

The simplest case to study first is the sample mean:

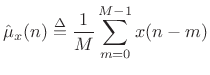$\displaystyle \hat{\mu}_x(n) \isdef \frac{1}{M}\sum_{m=0}^{M-1}x(n-m)$ (C.29)

Here we have defined the sample mean at time $ n$ as the average of the $ M$ successive samples up to time $ n$ --a ``running average''. The true mean is assumed to be the average over any infinite number of samples such as

$\displaystyle \mu_x = \lim_{M\to\infty}\hat{\mu}_x(n)$ (C.30)

or

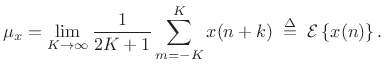$\displaystyle \mu_x = \lim_{K\to\infty}\frac{1}{2K+1}\sum_{m=-K}^{K}x(n+k) \isdefs {\cal E}\left\{x(n)\right\}.$ (C.31)

Now assume $ \mu_x=0$ , and let $ \sigma_x^2$ denote the variance of the process $ x(\cdot)$ , i.e.,

Var$\displaystyle \left\{x(n)\right\} \isdefs {\cal E}\left\{[x(n)-\mu_x]^2\right\} \eqsp {\cal E}\left\{x^2(n)\right\} \eqsp \sigma_x^2$ (C.32)

Then the variance of our sample-mean estimator $ \hat{\mu}_x(n)$ can be calculated as follows:

\begin{eqnarray*} \mbox{Var}\left\{\hat{\mu}_x(n)\right\} &\isdef & {\cal E}\left\{\left[\hat{\mu}_x(n)-\mu_x \right]^2\right\} \eqsp {\cal E}\left\{\hat{\mu}_x^2(n)\right\}\\ &=&{\cal E}\left\{\frac{1}{M}\sum_{m_1=0}^{M-1} x(n-m_1)\, \frac{1}{M}\sum_{m_2=0}^{M-1} x(n-m_2)\right\}\\ &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} {\cal E}\left\{x(n-m_1) x(n-m_2)\right\}\\ &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} r_x(\vert m_1-m_2\vert) \end{eqnarray*}

where we used the fact that the time-averaging operator $ {\cal E}\left\{\right\}$ is linear, and $ r_x(l)$ denotes the unbiased autocorrelation of $ x(n)$ . If $ x(n)$ is white noise, then $ r_x(\vert m_1-m_2\vert) = \sigma_x^2\delta(m_1-m_2)$ , and we obtain

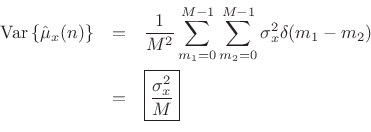
\begin{eqnarray*}\mbox{Var}\left\{\hat{\mu}_x(n)\right\} &=&\frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_2=0}^{M-1} \sigma_x^2\delta(m_1-m_2)\\ &=&\zbox {\frac{\sigma_x^2}{M}}\\ \end{eqnarray*}

We have derived that the variance of the $ M$ -sample running average of a white-noise sequence $ x(n)$ is given by $ \sigma_x^2/M$ , where $ \sigma_x^2$ denotes the variance of $ x(n)$ . We found that the variance is inversely proportional to the number of samples used to form the estimate. This is how averaging reduces variance in general: When averaging $ M$ independent (or merely uncorrelated) random variables, the variance of the average is proportional to the variance of each individual random variable divided by $ M$ .

Sample-Variance Variance

Consider now the sample variance estimator

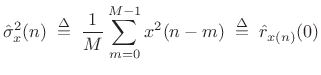$\displaystyle \hat{\sigma}_x^2(n) \isdefs \frac{1}{M}\sum_{m=0}^{M-1}x^2(n-m) \isdefs \hat{r}_{x(n)}(0)$ (C.33)

where the mean is assumed to be $ \mu_x ={\cal E}\left\{x(n)\right\}=0$ , and $ \hat{r}_{x(n)}(l)$ denotes the unbiased sample autocorrelation of $ x$ based on the $ M$ samples leading up to and including time $ n$ . Since $ \hat{r}_{x(n)}(0)$ is unbiased, $ {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} = {\cal E}\left\{\hat{r}_{x(n)}^2(0)\right\} = \sigma_x^2$ . The variance of this estimator is then given by

\begin{eqnarray*} \mbox{Var}\left\{\hat{\sigma}_x^2(n)\right\} &\isdef & {\cal E}\left\{[\hat{\sigma}_x^2(n)-\sigma_x^2]^2\right\}\\ &=& {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2-\sigma_x^4\right\} \end{eqnarray*}

where

\begin{eqnarray*} {\cal E}\left\{[\hat{\sigma}_x^2(n)]^2\right\} &=& \frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}{\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\}\\ &=& \frac{1}{M^2}\sum_{m_1=0}^{M-1}\sum_{m_1=0}^{M-1}r_{x^2}(\vert m_1-m_2\vert) \end{eqnarray*}

The autocorrelation of $ x^2(n)$ need not be simply related to that of $ x(n)$ . However, when $ x$ is assumed to be Gaussian white noise, simple relations do exist. For example, when $ m_1\ne m_2$ ,

$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = {\cal E}\left\{x^2(n-m_1)\right\}{\cal E}\left\{x^2(n-m_2)\right\}=\sigma_x^2\sigma_x^2= \sigma_x^4.$ (C.34)

by the independence of $ x(n-m_1)$ and $ x(n-m_2)$ , and when $ m_1=m_2$ , the fourth moment is given by $ {\cal E}\left\{x^4(n)\right\} = 3\sigma_x^4$ . More generally, we can simply label the $ k$ th moment of $ x(n)$ as $ \mu_k = {\cal E}\left\{x^k(n)\right\}$ , where $ k=1$ corresponds to the mean, $ k=2$ corresponds to the variance (when the mean is zero), etc.

When $ x(n)$ is assumed to be Gaussian white noise, we have

$\displaystyle {\cal E}\left\{x^2(n-m_1)x^2(n-m_2)\right\} = \left\{\begin{array}{ll} \sigma_x^4, & m_1\ne m_2 \\ [5pt] 3\sigma_x^4, & m_1=m_2 \\ \end{array} \right.$ (C.35)

so that the variance of our estimator for the variance of Gaussian white noise is

Var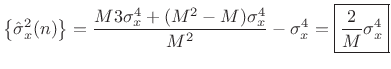$\displaystyle \left\{\hat{\sigma}_x^2(n)\right\} = \frac{M3\sigma_x^4 + (M^2-M)\sigma_x^4}{M^2} - \sigma_x^4 = \zbox {\frac{2}{M}\sigma_x^4}$ (C.36)

Again we see that the variance of the estimator declines as $ 1/M$ .

The same basic analysis as above can be used to estimate the variance of the sample autocorrelation estimates for each lag, and/or the variance of the power spectral density estimate at each frequency.

As mentioned above, to obtain a grounding in statistical signal processing, see references such as [201,121,95].

Next Section:
Gaussian Window and Transform
Previous Section:
Correlation Analysis