DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Lossless Filter Examples

The simplest lossless filter is a unit-modulus gain

$\displaystyle H(z) \eqsp e^{j\phi}$ (12.82)

where $ \phi$ can be any phase value. In the real case $ \phi$ can only be 0 or $ \pi$ , hence $ H(z)=\pm 1$ .

A lossless FIR filter can only consist of a single nonzero tap:

$\displaystyle H(z) \eqsp e^{j\phi} z^{-K} \protect$ (12.83)

for some fixed integer $ K$ , where $ \phi$ is again some constant phase, constrained to be 0 or $ \pi$ in the real-filter case. We consider only causal filters here, so $ K\geq 0$ .

Every finite-order, single-input, single-output (SISO), lossless IIR filter (recursive allpass filter) can be written as

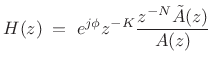$\displaystyle H(z) \eqsp e^{j\phi} z^{-K} \frac{z^{-N}{\tilde A}(z)}{A(z)}$ (12.84)

where 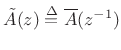$ K\geq 0$ , $ A(z) = 1 + a_1 z^{-1}+ a_2 z^{-2} + \cdots + a_N z^{-N}$ , and $ {\tilde A}(z)\isdef \overline{A}(z^{-1})$ . The polynomial $ {\tilde A}(z)$ can be obtained by reversing the order of the coefficients in $ A(z)$ , conjugating them, and multiplying by $ z^N$ . (The factor $ z^{-N}$ above serves to restore negative powers of $ z$ and hence causality.) Such filters are generally called allpass filters.

The normalized DFT matrix is an $ N\times N$ order zero paraunitary transformation. This is because the normalized DFT matrix, $ \bold{W}=[W_N^{nk}]/\sqrt{N}$ , $ n,k=0,\ldots,N-1$ , where $ W_N\isdeftext e^{-j2\pi/N}$ , is a unitary matrix:

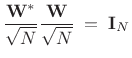$\displaystyle \frac{\bold{W}^\ast}{\sqrt{N}} \frac{\bold{W}}{\sqrt{N}} \eqsp \bold{I}_N$ (12.85)

Next Section:
Properties of Paraunitary Filter Banks
Previous Section:
Lossless Filters