DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Lossless Filters

To motivate the idea of paraunitary filters, let's first review some properties of lossless filters, progressing from the simplest cases up to paraunitary filter banks:

A linear, time-invariant filter $ H(z)$ is said to be lossless (or allpass) if it preserves signal energy. That is, if the input signal is $ x(n)$ , and the output signal is $ y(n) = (h\ast x)(n)$ , then we have

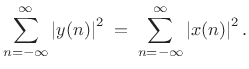$\displaystyle \sum_{n=-\infty}^{\infty} \left\vert y(n)\right\vert^2 \eqsp \sum_{n=-\infty}^{\infty} \left\vert x(n)\right\vert^2.$ (12.71)

In terms of the $ L2$ signal norm $ \left\Vert\,\,\cdot\,\,\right\Vert _2$ (§4.10.1), this can be expressed more succinctly as

$\displaystyle \left\Vert\,y\,\right\Vert _2^2 \eqsp \left\Vert\,x\,\right\Vert _2^2.$ (12.72)

Notice that only stable filters can be lossless since, otherwise, $ \left\Vert\,y\,\right\Vert=\infty$ . We further assume all filters are causal for simplicity.

It is straightforward to show that losslessness implies

$\displaystyle \left\vert H(e^{j\omega})\right\vert \eqsp 1, \quad \forall \omega.$ (12.73)

That is, the frequency response must have magnitude 1 everywhere on the unit circle in the $ z$ plane. Another way to express this is to write

$\displaystyle \overline{H(e^{j\omega})} H(e^{j\omega}) \eqsp 1, \quad\forall\omega,$ (12.74)

and this form generalizes to $ {\tilde H}(z)H(z)$ over the entire the $ z$ plane.

The paraconjugate of a transfer function may be defined as the analytic continuation of the complex conjugate from the unit circle to the whole $ z$ plane:

$\displaystyle {\tilde H}(z) \isdefs \overline{H}(z^{-1})$ (12.75)

where $ \overline{H}(z)$ denotes complex conjugation of the coefficients only of $ H(z)$ and not the powers of $ z$ . For example, if $ H(z)=1+jz^{-1}$ , then $ \overline{H}(z) = 1-jz^{-1}$ . We can write, for example,

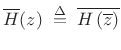$\displaystyle \overline{H}(z) \isdefs \overline{H\left(\overline{z}\right)}$ (12.76)

in which the conjugation of $ z$ serves to cancel the outer conjugation.

We refrain from conjugating $ z$ in the definition of the paraconjugate because $ \overline{z}$ is not analytic in the complex-variables sense. Instead, we invert $ z$ , which is analytic, and which reduces to complex conjugation on the unit circle.

The paraconjugate may be used to characterize allpass filters as follows:

A causal, stable, filter $ H(z)$ is allpass if and only if

$\displaystyle {\tilde H}(z) H(z) \eqsp 1.$ (12.77)

Note that this is equivalent to the previous result on the unit circle since

$\displaystyle {\tilde H}(e^{j\omega}) H(e^{j\omega}) \eqsp \overline{H}(1/e^{j\omega})H(e^{j\omega}) \eqsp \overline{H(e^{j\omega})}H(e^{j\omega}).$ (12.78)

To generalize lossless filters to the multi-input, multi-output (MIMO) case, we must generalize conjugation to MIMO transfer function matrices.

A $ p\times q$ transfer function matrix $ \bold{H}(z)$ is said to be lossless if it is stable and its frequency-response matrix $ \bold{H}(e^{j\omega})$ is unitary. That is,

$\displaystyle \bold{H}^*(e^{j\omega})\bold{H}(e^{j\omega}) \eqsp \bold{I}_q$ (12.79)

for all $ \omega$ , where $ \bold{I}_q$ denotes the $ q\times q$ identity matrix, and $ \bold{H}^\ast(e^{j\omega})$ denotes the Hermitian transpose (complex-conjugate transpose) of $ \bold{H}(e^{j\omega})$ :

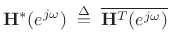$\displaystyle \bold{H}^*(e^{j\omega}) \isdefs \overline{\bold{H}^T(e^{j\omega})}$ (12.80)

Note that $ \bold{H}^*(e^{j\omega})\bold{H}(e^{j\omega})$ is a $ q\times q$ matrix product of a $ q\times p$ times a $ p\times q$ matrix. If $ q>p$ , then the rank must be deficient. Therefore, we must have $ p\geq q$ . (There must be at least as many outputs as there are inputs, but it's ok to have extra outputs.)

A lossless $ p\times q$ transfer function matrix $ \bold{H}(z)$ is paraunitary, i.e.,

$\displaystyle {\tilde {\bold{H}}}(z) \bold{H}(z) \eqsp \bold{I}_q$ (12.81)

Thus, every paraunitary matrix transfer function is unitary on the unit circle for all $ \omega$ . Away from the unit circle, paraunitary $ \bold{H}(z)$ is the unique analytic continuation of unitary $ \bold{H}(e^{j\omega})$ .

Next Section:
Lossless Filter Examples
Previous Section:
Example: Polyphase Analysis of the Weighted Overlap Add Case: 50% Overlap, Zero-Padding, and a Non-Rectangular Window