Review of STFT Filterbanks

Free Books Spectral Audio Signal Processing

Let's take a look at some of the STFT processors we've seen before, now viewed as polyphase filter banks. Since they all use FFTs to perform overlap-add decompositions of spectra, they are all efficient, but most are oversampled in time and/or frequency as ``filter banks'' go. Oversampling is usually preferred outside of a compression context, and normally required when spectral modifications are to be performed. The STFT also computes a uniform filter bank, but it can be used as the basis for a variety of non-uniform filter banks, as discussed in §10.7, to give frequency resolution more like that of hearing (§7.3).

For each selected STFT example below, a list of filter-bank properties is listed, followed by some discussion. Most of the properties are determined by the choice of FFT window and FFT hop size .

STFT, Rectangular Window, No Overlap

Perfect reconstruction
Critically sampled (relies on aliasing cancellation)
Poor channel isolation ( 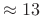$\approx 13$ dB)
Not robust to filter-bank modifications

This is the main critically sampled perfect-reconstruction filter bank implemented by an STFT (other examples involve Portnoff windows, §9.7). ``Filter-bank modifications'' here means modifications introduced as time-varying complex gains applied to the filter-bank channel signals prior to remodulation and summing to reconstruct the signal (Chapter 9). In contrast to this, as discussed in Chapter 8, multiplicative spectral modifications in overlap-add systems having sufficient time-domain zero-padding yield perfect reconstruction of the filtered signal, even when their filter-bank interpretation obviously involves aliasing cancellation among channels in the frequency domain.

STFT, Rectangular Window, 50% Overlap

Perfect reconstruction
Oversampled by 2 (less reliant on aliasing cancellation)
Poor channel isolation ( 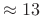$\approx 13$ dB)
Not very robust to filter-bank modifications, but better

Reducing the hop size to half the window length greatly reduces the amount of aliasing in the filter-bank output signals (§8.3.1). Recall that this happens because the folding frequency due to downsampling (by the hop size) doubles to coincide with the first zero-crossing of the window transform.

STFT, Triangular Window, 50% Overlap

Perfect reconstruction
Oversampled by 2
Better channel isolation ( 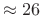$\approx 26$ dB)
Moderately robust to filter-bank modifications

This case is essentially the no-overlap rectangular-window case with the window-length doubled and the window-transform squared, as derived in Chapter 3. The squaring doubles the channel isolation in dB. To move the folding frequency out to the first zero-crossing, 75% overlap should be used ( $4\times$ oversampling in time).

STFT, Hamming Window, 75% Overlap

Perfect reconstruction
Oversampled by 4
Aliasing from side lobes only
Good channel isolation ( 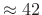$\approx 42$ dB)
Moderately robust to filter-bank modifications

This can be considered a ``telephone quality'' audio filter bank. It has been used many times to analyze/model speech signals.

STFT, Kaiser Window, Beta=10, 90% Overlap

Approximate perfect reconstruction (side lobes controlled by $\beta$ )
Oversampled by
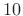
Excellent channel isolation ( 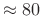$\approx 80$ dB)
Very robust to filter-bank modifications
Aliasing from side lobes only

Because the Kaiser window transform does not have harmonic nulls that can be tuned to harmonics of the frame rate (§8.3.1), we obtain only approximate perfect reconstruction. However, the reconstruction error is entirely under our control through the choice of the Kaiser-window $\beta$ parameter (determining its time-bandwidth product). This filter bank does not rely on aliasing cancellation (when side-lobes are negligible), so it is very robust to spectral modifications.

Sliding FFT (Maximum Overlap), Any Window, Zero-Padded by 5

Perfect reconstruction (always true when hop-size )
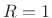Oversampled by 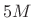, where

= window length (time-domain oversampling factor)

5 = zero-padding factor (frequency-domain oversampling factor)
Excellent channel isolation (set by window side lobes)
Extremely robust to filter-bank modifications
No aliasing to cancel!

This example is practical in research applications. With powerful computers and large disks, why not set the FFT hop size to and avoid all aliasing entirely? In the early days of computer music, this was the normal choice in phase-vocoder analysis for additive synthesis (§G.10), and it is of course far more affordable now. For aggressive spectral modifications, the sliding FFT ( ) generally yields the best quality results. Additionally, the signal analyzed can be oversampled so that the frequency domain has a large extended area where nonlinear distortion products can ``land'' without aliasing. As an example, ``tube distortion'' simulators routinely utilize $8\times$ or even $16\times$ oversampling in the input signal prior to distortion [300].

Next Section:
Wavelet Filter Banks
Previous Section:
MPEG Filter Banks