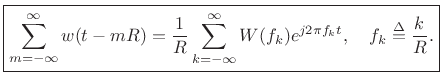DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Poisson Summation Formula

As shown in §B.14 above, the Fourier transform of an impulse train is an impulse train with inversely proportional spacing:

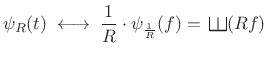$\displaystyle \psi_R(t)\;\longleftrightarrow\;{\frac{1}{R}}\cdot\psi_{\frac{1}{R}}(f) = \,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}(Rf)$ (B.56)

where

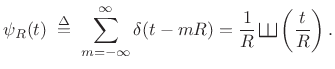$\displaystyle \psi_R(t) \isdefs \sum_{m=-\infty}^\infty \delta(t-mR) = \frac{1}{R}\,\raisebox{0.8em}{\rotatebox{-90}{\resizebox{1em}{1em}{\ensuremath{\exists}}}}\left(\frac{t}{R}\right).$ (B.57)

Using this Fourier theorem, we can derive the continuous-time PSF using the convolution theorem for Fourier transforms:B.1

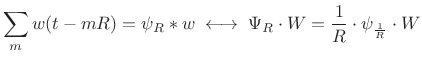$\displaystyle \sum_m w(t-mR) = \psi_R \ast w \;\longleftrightarrow\; \Psi_R \cdot W = \frac{1}{R}\cdot\psi_{\frac{1}{R}}\cdot W$ (B.58)

Using linearity and the shift theorem for inverse Fourier transforms, the above relation yields

\begin{eqnarray*} \sum_m w(t-mR) &=& \frac{1}{R} \hbox{\sc IFT}_t \left[W(f)\sum_k\delta\left(f-k\frac{1}{R}\right) \right] \quad\left(\mbox{define $f_k\isdef \frac{k}{R}$}\right) \\ [5pt] &=& \frac{1}{R} \hbox{\sc IFT}_t \left[\sum_k W(f_k)\cdot\delta\left(f-f_k\right) \right]\\ [5pt] &=& \frac{1}{R} \sum_k W(f_k)\cdot\hbox{\sc IFT}_t \left[\delta\left(f-f_k\right) \right]\\ [5pt] &=& \frac{1}{R} \sum_k W(f_k)e^{j 2\pi f_k t}. \end{eqnarray*}

We have therefore shown

$\displaystyle \zbox {\sum_{m=-\infty}^{\infty} w(t-mR) = \frac{1}{R} \sum_{k=-\infty}^{\infty} W(f_k)e^{j 2\pi f_k t}, \quad f_k\isdef \frac{k}{R}.} \protect$ (B.59)

Compare this result to Eq.$ \,$ (8.30). The left-hand side of (B.60) can be interpreted $ s_R(t)=\hbox{\sc Alias}_R(w)$ , i.e., the time-alias of $ w$ on a block of length $ R$ . The function $ s_R(t)$ is periodic with period $ R$ seconds. The right-hand side of (B.60) can be interpreted as the inverse Fourier series of $ W(f)$ sampled at intervals of $ 1/R$ Hz. This sampling of $ W(\omega)$ in the frequency domain corresponds to the aliasing of $ w(t)$ in the time domain.

Next Section:
Sampling Theory
Previous Section:
Impulse Trains