Free Books
   Free Books    Spectral Audio Signal Processing  

Polyphase Decomposition

The previous section derived an efficient polyphase implementation of an FIR filter $ h$ whose output was downsampled by the factor $ N$ . The derivation was based on commuting the downsampler with the FIR summer. We now derive the polyphase representation of a filter of any length algebraically by splitting the impulse response $ h$ into $ N$ polyphase components.

Two-Channel Case

The simplest nontrivial case is $ N=2$ channels. Starting with a general linear time-invariant filter

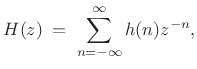$\displaystyle H(z) \eqsp \sum_{n=-\infty}^{\infty}h(n)z^{-n},$ (12.6)

we may separate the even- and odd-indexed terms to get

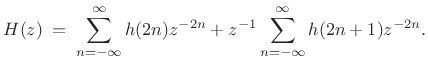$\displaystyle H(z) \eqsp \sum_{n=-\infty}^{\infty}h(2n)z^{-2n} + z^{-1}\sum_{n=-\infty}^{\infty}h(2n+1)z^{-2n}.$ (12.7)

We define the polyphase component filters as follows:

\begin{eqnarray*} E_0(z)&=&\sum_{n=-\infty}^{\infty}h(2n)z^{-n}\\ [5pt] E_1(z)&=&\sum_{n=-\infty}^{\infty}h(2n+1)z^{-n} \end{eqnarray*}

$ E_0(z)$ and $ E_1(z)$ are the polyphase components of the polyphase decomposition of $ H(z)$ for $ N=2$ .

Now write $ H(z)$ in terms of its polyphase components:

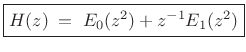$\displaystyle \zbox {H(z) \eqsp E_0(z^2) + z^{-1}E_1(z^2)}$ (12.8)

As a simple example, consider

$\displaystyle H(z)\eqsp 1 + 2z^{-1} + 3z^{-2} + 4z^{-3}.$ (12.9)

Then the polyphase component filters are

\begin{eqnarray*} E_0(z) &=& 1 + 3z^{-1}\\ [5pt] E_1(z) &=& 2 + 4z^{-1} \end{eqnarray*}

and

$\displaystyle H(z) \eqsp E_0(z^2) + z^{-1}E_1(z^2) \eqsp (1 + 3z^{-2}) + (2z^{-1} + 4z^{-3}).$ (12.10)

N-Channel Polyphase Decomposition

Figure 11.9: Schematic illustration of three interleaved polyphase signal components.
\includegraphics[scale=0.8]{eps/polytime}

For the general case of arbitrary $ N$ , the basic idea is to decompose $ x(n)$ into its periodically interleaved subsequences, as indicated schematically in Fig.11.9. The polyphase decomposition into $ N$ channels is given by

$\displaystyle H(z) \eqsp \sum_{l=0}^{N-1} z^{-l}E_l(z^N) \protect$ (12.11)

where the subphase filters are defined by

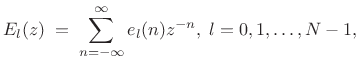$\displaystyle E_l(z) \eqsp \sum_{n=-\infty}^{\infty}e_l(n)z^{-n},\; l=0,1,\ldots,N-1,$ (12.12)

with

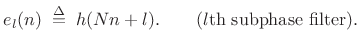$\displaystyle e_l(n) \isdefs h(Nn+l). \qquad\hbox{($l$th subphase filter)}.$ (12.13)

The signal $ e_l(n)$ can be obtained by passing $ h(n)$ through an advance of $ l$ samples, followed by downsampling by the factor $ N$ . as shown in Fig.11.10.


\begin{psfrags} % latex2html id marker 29755\psfrag{M}{{\normalsize $N$}}\psfrag{ztl}{{\Large $z^l$}}\psfrag{h[n]}{{\Large $h(n)$}}\psfrag{eln}{{\Large $e_l(n)$}}\begin{figure}[htbp] \includegraphics[width=0.5\twidth]{eps/polypick} \caption{Advance by $l$\ samples followed by a downsampling by the factor $N$.} \end{figure} \end{psfrags}

Type II Polyphase Decomposition

The polyphase decomposition of $ H(z)$ into $ N$ channels in (11.11) may be termed a ``type I'' polyphase decomposition. In the ``type II'', or reverse polyphase decomposition, the powers of $ z$ progress in the opposite direction:

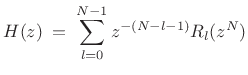$\displaystyle H(z) \eqsp \sum_{l=0}^{N-1} z^{-(N-l-1)} R_{l}(z^{N})$ (12.14)

We will see that we need type I for analysis filter banks and type II for synthesis filter banks in a general ``perfect reconstruction filter bank'' analysis/synthesis system.

Filtering and Downsampling, Revisited

Let's return to the example of §11.1.3, but this time have the FIR lowpass filter h(n) be length $ M=LN$ , $ L\in{\bf Z}$ . In this case, the $ N$ polyphase filters, $ e_l(n)$ , are each length $ L$ .12.2 Recall that

$\displaystyle H(z) \eqsp E_0(z^N) + z^{-1}E_1(z^N) + \cdots + z^{-(N-1)}E_{N-1}(z^N)$ (12.15)

leading to the result shown in Fig.11.11.

Figure: Polyphase decomposition of a length $ M=LN$ FIR filter followed by a downsampler.
\includegraphics[width=0.7\twidth]{eps/down_FIR_poly}

Figure: Polyphase decomposition of a length $ M=LN$ FIR filter followed by a downsampler.
\includegraphics[width=0.7\twidth]{eps/down_FIR_poly_com}

Next, we commute the $ N$ :$ 1$ downsampler through the adders and upsampled (stretched) polyphase filters $ E_l(z^N)$ to obtain Fig.11.12. Commuting the downsampler through the subphase filters $ E_l(z^N)$ to obtain $ E_l(z)$ is an example of a multirate noble identity.

Multirate Noble Identities

Figure 11.13 illustrates the so-called noble identities for commuting downsamplers/upsamplers with ``sparse transfer functions'' that can be expressed a function of $ z^{-N}$ . Note that downsamplers and upsamplers are linear, time-varying operators. Therefore, operation order is important. Also note that adders and multipliers (any memoryless operators) may be commuted across downsamplers and upsamplers, as shown in Fig.11.14.


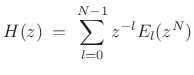
\begin{psfrags} % latex2html id marker 29805\psfrag{nd}{ $N\downarrow$\ }\psfrag{hz}{ $H(z)$\ }\psfrag{hzn}{ $H(z^N)$\ }\psfrag{equal}{ $\equiv$\ }\begin{figure}[htbp] \includegraphics[width=0.9\twidth]{eps/noble} \caption{Multirate noble identities} \end{figure} % was 6in \end{psfrags}

Figure 11.14: Commuting of downsampler with adder and gains.
\includegraphics[width=0.9\twidth]{eps/noble_commute}

Next Section:
Critically Sampled Perfect Reconstruction Filter Banks
Previous Section:
Upsampling and Downsampling