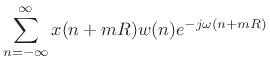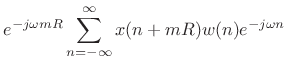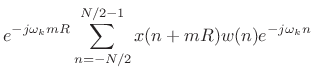Free Books
   Free Books    Spectral Audio Signal Processing  

Practical Computation of the STFT

While the definition of the STFT in (7.1) is useful for theoretical work, it is not really a specification of a practical STFT. In practice, the STFT is computed as a succession of FFTs of windowed data frames, where the window ``slides'' or ``hops'' forward through time. We now derive such an implementation of the STFT from its mathematical definition.

The STFT in (7.1) can be rewritten, adding 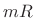$ mR$ to $ n$ , as

$\displaystyle X_m(\omega)$ $\displaystyle =$ $\displaystyle \sum_{n=-\infty}^{\infty} x(n+mR) w(n) e^{-j\omega (n+mR)}$  
  $\displaystyle =$ $\displaystyle e^{-j\omega mR} \sum_{n=-\infty}^{\infty} x(n+mR) w(n) e^{-j\omega n}$  
  $\displaystyle =$ $\displaystyle e^{-j\omega mR}\hbox{\sc DTFT}_\omega(\hbox{\sc Shift}_{-mR}(x) \cdot w). \protect$ (8.3)

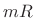
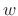
In this form, the data centered about time $ mR$ are translated to time 0, multiplied by the (let's assume zero-phase) window $ w$ , and then the DTFT is performed. Since the nonzero portion of the windowed data is centered on time zero, the DTFT can be replaced by the DFT (or FFT). This effectively samples the DTFT in frequency. This sampling will not cause (time) aliasing if the number of samples around the unit circle is greater than the width (in samples) of the time interval including all nonzero datapoints. 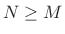In other words, sampling the frequency axis is information-preserving when the signal is properly time limited.8.3Let $ M$ denote the window length (typically an odd number) and $ N\geq M$ be the DFT length (typically a power of 2). 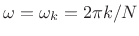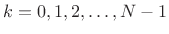Then sampling (7.3) at $ \omega=\omega_k= 2\pi k/N$ , $ k=0,1,2,\ldots,N-1$ , and using the fact that the window $ w(n)$ is time-limited to less than $ N$ samples centered about time zero, yields
$\displaystyle X_m(\omega_k)$ $\displaystyle =$ $\displaystyle e^{-j\omega_k mR}\sum_{n=-N/2}^{N/2-1} x(n+mR) w(n) e^{-j\omega_k n}$  
  $\displaystyle =$ $\displaystyle e^{-j\omega_k mR}\hbox{\sc DFT}_{N,\omega_k}(\hbox{\sc Shift}_{-mR}(x) \cdot w). \protect$ (8.4)

Since indexing in the DFT is modulo $ N$ , the sum over $ n$ can be ``rotated'' to a sum from 0 to $ N-1$ as is conventionally implemented for the DFT. In practice, this means that the right half of the windowed data frame goes at the beginning of the FFT input buffer, and the left half of the windowed frame goes at the end, with zero-padding in the middle (see Fig.2.6b on page [*] for an illustration).

Next Section:
Summary of STFT Computation Using FFTs
Previous Section:
Mathematical Definition of the STFT