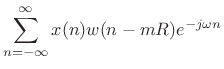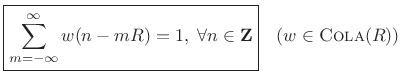DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Mathematical Definition of the STFT

The usual mathematical definition of the STFT is [9]

$\displaystyle X_m(\omega)$ $\displaystyle =$ $\displaystyle \sum_{n=-\infty}^{\infty} x(n) w(n-mR) e^{-j\omega n}$  
  $\displaystyle =$ $\displaystyle \hbox{\sc DTFT}_\omega(x\cdot\hbox{\sc Shift}_{mR}(w)), \protect$ (8.1)

where

\begin{eqnarray*} x(n) &=& \hbox{input signal at time $n$}\\ w(n) &=& \hbox{length $M$\ window function (\textit{e.g.}, Hamming)}\\ X_m(\omega) &=& \hbox{DTFT of windowed data centered about time $mR$}\\ R &=& \hbox{hop size, in samples, between successive DTFTs.}\\ \end{eqnarray*}

If the window $ w(n)$ has the Constant OverLap-Add (COLA) property at hop-size $ R$ , i.e., if

$\displaystyle \zbox {\sum_{m=-\infty}^{\infty} w(n-mR) = 1, \; \forall n\in{\bf Z}} \quad\mbox{($w\in\hbox{\sc Cola}(R)$)} \protect$ (8.2)

then the sum of the successive DTFTs over time equals the DTFT of the whole signal $ X(\omega)$ :

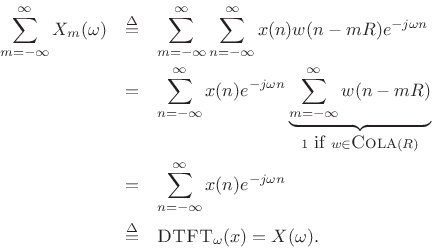
\begin{eqnarray*} \sum_{m=-\infty}^\infty X_m(\omega) &\isdef & \sum_{m=-\infty}^\infty\sum_{n=-\infty}^{\infty} x(n) w(n-mR) e^{-j\omega n}\\ &=& \sum_{n=-\infty}^{\infty} x(n) e^{-j\omega n} \underbrace{\sum_{m=-\infty}^\infty w(n-mR)}_{1\hbox{ if }w\in\hbox{\sc Cola}(R)} \\ &=& \sum_{n=-\infty}^{\infty} x(n) e^{-j\omega n} \\ &\isdef & \hbox{\sc DTFT}_\omega(x) = X(\omega). \end{eqnarray*}

We will say that windows satisfying $ \sum_m w(n-mR) = 1$ (or some constant) for all $ n\in{\bf Z}$ are said to be $ \hbox{\sc Cola}(R)$ . For example, the length $ M$ rectangular window is clearly $ \hbox{\sc Cola}(M)$ (no overlap). The Bartlett window and all windows in the generalized Hamming family (Chapter 3) are $ \hbox{\sc Cola}(M/2)$ (50% overlap), when the endpoints are handled correctly.8.1 A $ \hbox{\sc Cola}(M/2)$ example is depicted in Fig.8.9. Any window that is $ \hbox{\sc Cola}(R)$ is also $ \hbox{\sc Cola}(R/k)$ , for $ k=2,3,4,\ldots,R$ , provided $ R/k$ is an integer.8.2 We will explore COLA windows more completely in Chapter 8.

When using the short-time Fourier transform for signal processing, as taken up in Chapter 8, the COLA requirement is important for avoiding artifacts. For usage as a spectrum analyzer for measurement and display, the COLA requirement can often be relaxed, as doing so only means we are not weighting all information equally in our analysis. Nothing disastrous happens, for example, if we use 50% overlap with the Blackman window in a short-time spectrum analysis over time--the results look fine; however, in such a case, data falling near the edges of the window will have a slightly muted impact on the results relative to data falling near the window center, because the Blackman window is not COLA at 50% overlap.

Next Section:
Practical Computation of the STFT
Previous Section:
Example: Pink Noise Analysis