Summary of STFT Computation Using FFTs

Free Books Spectral Audio Signal Processing

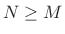Read samples of the input signal into a local buffer of length $N\geq M$ which is initially zeroed

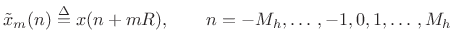
$\displaystyle \tilde{x}_m(n) \isdef x(n+mR), \qquad n=-M_h, \ldots\,,-1,0,1,\ldots\,, M_h$

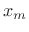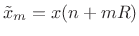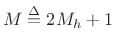We call the th frame of the input signal, and $\tilde{x}_m=x(n+mR)$ the th time normalized input frame (time-normalized by translating it to time zero). The frame length is $M\isdef 2M_h+1$ , which we assume to be odd for reasons to be discussed later. The time advance (in samples) from one frame to the next is called the hop size or step size.
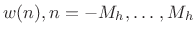Multiply the data frame pointwise by a length spectrum analysis window $w(n), n=-M_h,\ldots\,,M_h$ to obtain the th windowed data frame (time normalized):

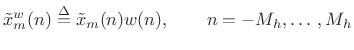
$\displaystyle \tilde{x}_m^w(n) \isdef \tilde{x}_m(n) w(n), \qquad n=-M_h,\ldots\,,M_h$
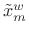Extend $\tilde{x}_m^w$ with zeros on both sides to obtain a zero-padded frame:

$\displaystyle \tilde{x}_m^{w,z}(n) \isdef \left\{\begin{array}{ll} \tilde{x}_m^w(n), & \left\vert n\right\vert\leq M_h\isdef {\frac{M-1}{2}} \\ [5pt] 0, & M_h< n \leq {\frac{N}{2}}-1 \\ [5pt] 0, & -{\frac{N}{2}}\leq n < -M_h \\ \end{array} \right.$ (8.5)

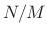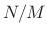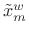where is chosen to be a power of two larger than . The number is the zero-padding factor. As discussed in §2.5.3, the zero-padding factor is the interpolation factor for the spectrum, i.e., each FFT bin is replaced by bins, interpolating the spectrum using ideal bandlimited interpolation [264], where the ``band'' in this case is the -sample nonzero duration of $\tilde{x}_m^w$ in the time domain.
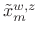Take a length FFT of $\tilde{x}_m^{w,z}$ to obtain the time-normalized, frequency-sampled STFT at time :

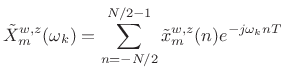
$\displaystyle \tilde{X}_m^{w,z}(\omega_k )=\sum _{n=-N/2}^{N/2-1} \tilde{x}_m^{w,z}(n) e^{-j\omega_k n T}$ (8.6)

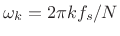where $\omega_k = 2\pi k f_s / N$ , and 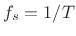is the sampling rate in Hz. As in any FFT, we call the bin number.
If needed, time normalization may be removed using a linear phase term to yield the sampled STFT:

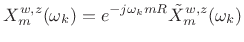
$\displaystyle X^{w,z}_m(\omega_k) = e^{-j\omega_k mR}\tilde{X}_m^{w,z}(\omega_k )$ (8.7)

The (continuous-frequency) STFT may be approached arbitrarily closely by using more zero padding and/or other interpolation methods.
Note that there is no irreversible time-aliasing when the STFT frequency axis $\omega$ is sampled to the points $\omega_k$ , provided the FFT size is greater than or equal to the window length .