DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Rectangular Window Side-Lobes

From Fig.3.3 and Eq.$ \,$ (3.4), we see that the main-lobe width is $ 2\cdot 2\pi/M=4\pi/11 \approx 1.1$ radian, and the side-lobe level is 13 dB down.

Since the DTFT of the rectangular window approximates the sinc function (see (3.4)), which has an amplitude envelope proportional to $ 1/\omega$ (see (3.7)), it should ``roll off'' at approximately 6 dB per octave (since $ -20\log_{10}(2)=6.0205999\ldots$ ). This is verified in the log-log plot of Fig.3.6.

Figure 3.6: Roll-off of the rectangular-window Fourier transform.
\includegraphics[width=\textwidth ]{eps/rectWindowLLFT}

As the sampling rate approaches infinity, the rectangular window transform ( $ \hbox{asinc}$ ) converges exactly to the sinc function. Therefore, the departure of the roll-off from that of the sinc function can be ascribed to aliasing in the frequency domain, due to sampling in the time domain (hence the name `` $ \hbox{asinc}$ '').

Note that each side lobe has width $ \Omega_M \isdeftext 2\pi/M$ , as measured between zero crossings.4.3 The main lobe, on the other hand, is width $ 2\Omega_M$ . Thus, in principle, we should never confuse side-lobe peaks with main-lobe peaks, because a peak must be at least $ 2\Omega_M$ wide in order to be considered ``real''. However, in complicated real-world scenarios, side-lobes can still cause estimation errors (``bias''). Furthermore, two sinusoids at closely spaced frequencies and opposite phase can partially cancel each other's main lobes, making them appear to be narrower than $ 2\Omega_M$ .

In summary, the DTFT of the $ M$ -sample rectangular window is proportional to the `aliased sinc function':

\begin{eqnarray*} \hbox{asinc}_M(\omega) &\isdef & \frac{\sin(\omega M / 2)}{M\cdot\sin(\omega/2)} \\ [0.2in] &\approx& \frac{\sin(\pi fM)}{M\pi f} \isdefs \mbox{sinc}(fM) \end{eqnarray*}

Thus, it has zero crossings at integer multiples of

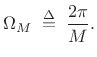$\displaystyle \Omega_M \isdefs \frac{2\pi}{M}.$ (4.11)

Its main-lobe width is $ 2\Omega_M$ and its first side-lobe is 13 dB down from the main-lobe peak. As $ M$ gets bigger, the main-lobe narrows, giving better frequency resolution (as discussed in the next section). Note that the window-length $ M$ has no effect on side-lobe level (ignoring aliasing). The side-lobe height is instead a result of the abruptness of the window's transition from 1 to 0 in the time domain. This is the same thing as the so-called Gibbs phenomenon seen in truncated Fourier series expansions of periodic waveforms. The abruptness of the window discontinuity in the time domain is also what determines the side-lobe roll-off rate (approximately 6 dB per octave). The relation of roll-off rate to the smoothness of the window at its endpoints is discussed in §B.18.

Next Section:
Rectangular Window Summary
Previous Section:
Zero-Phase Zero Padding