STFT Summary and Conclusions
The Short-Time Fourier Transform (STFT) may be viewed either as an OverLap-Add (OLA) processor, or as a Filter-Bank Sum (FBS). We derived two conditions for perfect reconstruction which are Fourier duals of each other:
- For OLA, the window must overlap-add to a constant in the time
domain. By the Poisson summation formula, this is equivalent
to having window transform nulls at all nonzero multiples of
the frame rate
.
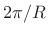- For FBS, the window transform must overlap-add to a
constant in the frequency domain, and this is equivalent to
having window nulls in the time domain at all nonzero multiples
of the transform size
.
In general, STFT filter banks are oversampled except when using
the rectangular window of length 
and a hop size 
. Critical
sampling is desirable for compression systems, but this can be
problematic when spectral modifications are contemplated
(adjacent-channel aliasing no longer canceled).
STFT filter banks are uniform filter banks, as opposed ``constant Q''. In some audio applications, it is preferable to use non-uniform filter banks which approximate the auditory filter bank. Approximate constant-Q filter banks are easily synthesized from STFT filter banks by summing adjacent frequency channels, as detailed in §10.7 below. Additional pointers can be found in Appendix E. We will look at a particular octave filter bank when we talk about wavelet filter banks (§11.9).
Next Section:
Fundamental Frequency Estimation from Spectral Peaks
Previous Section:
STFT with Modifications
