Scaling Theorem
The scaling theorem (or similarity theorem) says that if
you horizontally ``stretch'' a signal by the factor ![]() in the
time domain, you ``squeeze'' and amplify its Fourier transform by the
same factor in the frequency domain. This is an important general
Fourier duality relationship:
in the
time domain, you ``squeeze'' and amplify its Fourier transform by the
same factor in the frequency domain. This is an important general
Fourier duality relationship:
Theorem: For all continuous-time functions ![]() possessing a Fourier
transform,
possessing a Fourier
transform,
where
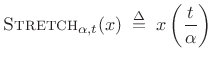
and
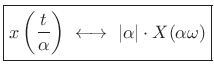 |
(3.41) |
Proof: See §B.4.
The scaling theorem is fundamentally restricted to the
continuous-time, continuous-frequency (Fourier transform) case. The
closest we come to the scaling theorem among the DTFT theorems
(§2.3) is the stretch (repeat) theorem
(page ![]() ). For this and other continuous-time Fourier
theorems, see Appendix B.
). For this and other continuous-time Fourier
theorems, see Appendix B.
Next Section:
Spectral Roll-Off
Previous Section:
Differentiation Theorem Dual



















