A New Contender in the Quadrature Oscillator Race

This blog advocates a relatively new and interesting quadrature oscillator developed by A. David Levine in 2009 and independently by Martin Vicanek in 2015 [1]. That oscillator is shown in Figure 1.

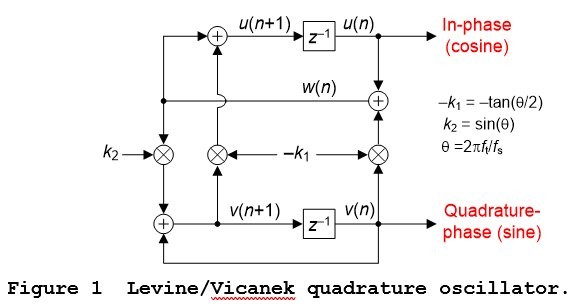
The time domain equations describing the Figure 1 oscillator are

     w(n) = u(n)-k₁v(n).                                                                         (1)

     u(n+1) = w(n)-k₁v(n+1).                                                                 (2)

     v(n+1) = v(n) + k₂w(n).                                                                  (3)

The coefficients k₁ and k₂ are

     k₁ = tan($\theta$/2),                                                                                 (4a)

     k₂ = sin($\theta$),                                                                                     (4b)

and

     $\theta$ = 2$\pi$f_t/f_s radians,                                                                       (4c)

where f_t is the oscillator’s tuned frequency (in Hz) and f_s is the data sample rate (in Hz).

The Merits of the Levine/Vicanek Oscillator

Relative to the two traditional quadrature oscillators described in Appendix A the Levine/Vicanek oscillator has several advantageous properties. The oscillator:

• Has good tuned frequency accuracy at low frequencies,

• Its computational workload is reasonable, and

• It is a guaranteed stable oscillator.

Oscillator Implementation

In software the Figure 1 Levine/Vicanek oscillator is implemented by

    Step# 1: Defining coefficients k₁ and k₂,

    Step# 2: For n = 0 set the two outputs to u(0) = 1 and v(0) = 0.

    Step# 3: Using v(0) and u(0) compute w(1),

    Step# 4: Using v(0) and w(1) compute v(1),

    Step# 5: Using w(1) and v(1) compute u(1),

    Step# 6: Using v(1) and u(1) compute w(2),

    Step# 7: Using v(1) and w(2) compute v(2),     

    Step# 8: Using w(2) and v(2) compute u(2),

and so on.

Additional Information

To add to the material provided here and in Reference [1], the PDF file associated with this blog provides additional information. That file’s Appendix B derives the transfer functions of the Levine/Vicanek quadrature oscillator and its Appendix C provides an algebraic proof of the oscillator’s guaranteed stability.

Conclusion

This blog publicized the beneficial properties of the Levine/Vicanek quadrature oscillator. That oscillator’s straightforward implementation and guaranteed stability make it a useful candidate for applications requiring a quadrature oscillator.

Postscript

Vicanek developed his quadrature oscillator in 2015. After I initially wrote this blog I learned that A. David Levine (inventor, musician, and musical technologist extraordinaire) developed a quadrature oscillator mathematically equivalent to Vicanek’s in 2009. Levine, a DSP engineer who actually knows which end of a soldering iron is hot, used his oscillator in a commercial hardware product described at the following website: https://muzemazer.com/mmcv

References

[1] M. Vicanek, “A New Recursive Quadrature Oscillator”,
    October, 2015, Available online at:
    https://www.vicanek.de/articles.htm

[2] Frerking, M., Digital Signal Processing in Communications Systems,
    Chapman & Hall, 1994, pp. 214-217.

[3] R. Lyons, Understanding Digital Signal Processing,
    3rd Ed., Prentice Hall, Englewood Cliffs, New Jersey, 2011,
    pp. 834-835.

[4] C. M. Rader and B. Gold, “Effects of Parameter Quantization on the
    Poles of Digital a Filter”, Proceedings of the IEEE,  Vol. 55,
    May 1967, pp. 688-689.

[5] S. Mitra, "Digital Signal Processing", 4th Edition, McGraw Hill
    Publishing, 2011, pp. 674-675.

[6] J. Proakis and D. Manolakis, Digital Signal Processing-
    Principles, Algorithms, and Applications, 3rd Ed., Prentice
    Hall, Upper Saddle River, New Jersey, 1996, pp. 574–576.

[7] A. Oppenheim and R. Schafer, Discrete-Time Signal Processing,
    2nd Ed., Prentice Hall, Englewood Cliffs, New Jersey, 1999,
    pp. 382–384.

[8] C. Turner, “Recursive Discrete-Time Sinusoidal Oscillators”,
    Available online at: http://claysturner.com/

[9] R. Lyons, Understanding Digital Signal Processing,
    3rd Ed., Prentice Hall, Englewood Cliffs, New Jersey, 2011,
    pp. 786-789.

Appendix A: Two Common 2nd-Order Quadrature Oscillators

To help us appreciate the novel Vicanek quadrature oscillator this appendix gives a brief description of the properties of two traditional quadrature oscillators that have been previously presented in the literature of DSP.

Those two well-known quadrature oscillators, based on 2nd-order resonators, are shown in Figure A-1.

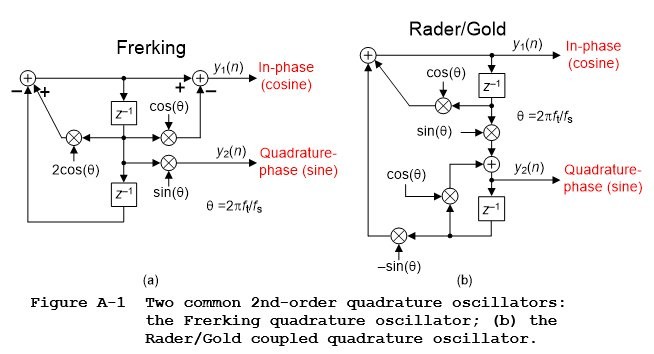
The Frerking oscillator in Figure A-1(a) is based upon the well-known 2nd-order IIR resonator that’s described in Reference [2]. While its outputs are guaranteed stable (the oscillator’s z-domain poles always lie on the z-plane’s unit circle) this oscillator’s tuned frequency accuracy depends on the tuned frequency—and that accuracy is poor at low frequencies.

The Rader/Gold oscillator in Figure A-1(b) is based upon the so called “coupled” 2nd-order IIR resonator so thoroughly covered in the literature of DSP [3‑7]. That’s why this oscillator is called a “coupled quadrature” oscillator. Happily this oscillator has good frequency control at low frequencies but, sadly, its output’s amplitudes are not stable. With quantized coefficients this oscillator’s z-domain poles never lie exactly on the z-plane’s unit circle, except at a frequency of $\theta$ = $\pi$/2 radians/sample (one quarter of the data sample rate).

I’ll verify my statement regarding Rader/Gold coupled oscillator’s instability with the following not so well-known facts. The oscillator’s y₂(n) output has a z-domain transfer function of:

$$H_{y2}(z)=\frac{Y_{y2}(z)}{X(z)}= {sin({\theta})z^{-1}\over 1-2cos({\theta})z^{-1}+[ {cos^2({\theta})}+ {sin^2({\theta})} ]z^{-2}}.\qquad(A-1)$$

The [cos²($\theta$) + sin²($\theta$)] factor in Eq. (A-1) is the sum of the Figure A-1(b) oscillator's coefficients values squared. And in practice those oscillator cos($\theta$) and sin($\theta$) coefficients are quantized and will be incorrect by some small quantization error.

Based on the Viète’s Formula test described in Appendix C of the PDF file associated with this blog, for a 2nd-order oscillator to be guaranteed stable its transfer function denominator’s z^-2 coefficient must be unity. Keeping in mind that the oscillator's cos($\theta$) and sin($\theta$) coefficients are quantized, H_y2(z)’s [cos²($\theta$) + sin²($\theta$)] factor will never be unity with slightly incorrect cos²($\theta$) and sin²($\theta$) values, except at a frequency of $\theta$ = $\pi$/2 radians/sample.

For completeness I mention that DSP wizard Clay Turner developed an automatic gain control (AGC) network to be used with the coupled quadrature oscillator [8‑9]. But that AGC network significantly increases the resultant oscillator’s computational workload.

Sign in