Hello,

this article is meant to give a quick overview over polyphase filtering and Farrows interpolation.

A good reference with more depth is for example Fred Harris' paper: http://www.signumconcepts.com/IP_center/paper018.pdf

The task is as follows:
Interpolate a band-limited discrete-time signal at a variable offset between samples.
In other words:
Delay the signal by a given amount with sub-sample accuracy.
Both mean the same.

The picture below shows samples (black) representing a continuous-time waveform (blue).

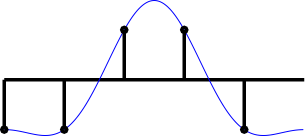
Conceptually, the problem is "easy" to solve:

Reconstruct the continuous-time waveform from the samples,
then
resample as desired

Ideal reconstruction of the blue curve requires an ideal lowpass filter. It can be approximated by a FIR filter to any desired accuracy (but the better the filter, the more latency is introduced to the system).

Another approximation can be made: Instead of delaying the signal in arbitrary small steps, it may be sufficient to limit the accuracy to a fraction 1/N of a sample. In my example I'm using 1/8.
This limitation will be lifted at the end, when the polyphase filter is developed into the Farrows interpolator.

Accordingly, the task is now:
Interpolate the signal by a factor of N (in the example 8)
and
decimate with an offset according to the delay, also called "decimation phase".

Interpolation is done by inserting zero samples... (picture)

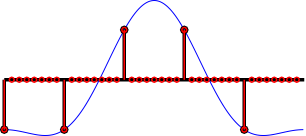
... and lowpass-filtering (picture).

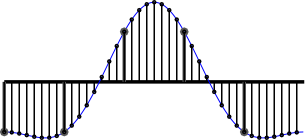
Out of N samples, the one with the desired offset is now picked out. The other N-1 samples are discarded by decimation.

For example: decimation for a 1/8 offset, only the red samples 'survive':

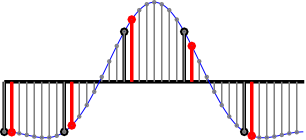
Alternative decimation phase: Delay 2/8 samples, the green samples are of interest:

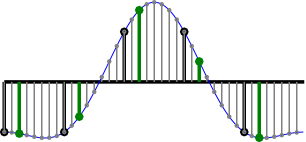
Another decimation phase for 3/8 samples delay (blue samples)

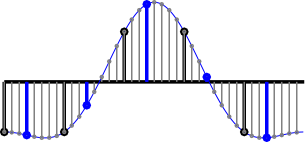
A possible FIR filter implementing the lowpass and decimation is shown below:
For the 1/8 delay case, only the red taps are nonzero, the other samples are discarded (decimated):
Delay by 2/8 uses only the green taps, delay by 3/8 only the blue taps and so on.

A real FIR filter designed to typical requirements (most notably passband ripple, alias rejection, width of the transition region), may easily require 100 taps or more. It will be much longer than shown.

Of course, an implementation according to above picture would be very inefficient, since most parts of the filter aren't doing anything (not contributing to the output).
This can be seen in the following picture, showing the same filter with all "decimated" branches removed.

Only one out of 8 taps is nonzero. Also, N-1 zero samples are created at the input for every actual sample, and they cannot contribute to the output.
As a result, the filter can be simplified, and the N-1 zero samples per input sample are omitted.
The picture below shows three filters for different decimation phase, delaying the signal by 1/8, 2/8 or 3/8 of a sample, respectively.

Note that in comparison to the full-length FIR filter, the length has shrunk by a factor of N (8 in the example). Only one of the above filters is needed at a time. So one filter is sufficient, with N banks of coefficients that are selected by a "commutator switch".

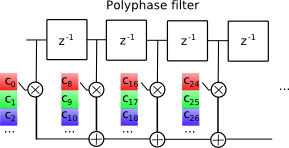
Even though the number of delays and multipliers has been reduced, the total number of coefficients remains the same as in the original filter.

The higher the required subsample accuracy N, the more coefficients are needed.
Instead of stacking more and more coefficients for each multiplier, it is possible to fit one polynomial to the series of coefficients for each multiplier. Its variable is the desired subsample delay, corresponding to the position of the commutator switch in the above picture.

The Farrows interpolator replaces each column of coefficients with a polynomial.

So much for now...
I hope the material has been useful to give some overview on the topic.
If you have comments or questions, please reply to the blog or send me a mail.
Especially "bug reports" are always welcome.
And thanks for reading!

Cheers

Markus

Another free reference: http://www.acoustics.hut.fi/~vpv/publications/icassp00-fd.pdf

PS: Be careful with using equiripple filter designs (Parks McClellan) for Farrows scheme.
The outermost points of the impulse response do not form a "smooth" curve. They are a discontinuity and cannot be easily approximated by a polynomial.
This issue does not appear with a simple polyphase implementation of the same filter.

Some related code snippets:

Determining the delay between two given signals and resampling

Farrow resampler implementation in plain Matlab (vectorized, no toolboxes)

Farrow resampler implementation in C (sample-by-sample)

Ideal resampling at arbitrary time instants

Bank-switched Farrow resampler: (documented here): Fewer multiplications at the expense of more coefficients