Bank-switched Farrow resampler

Posted by Markus Nentwig on Aug 13 2011 under Matlab | Basics | Multirate DSP   

Bank-switched Farrow resampler

Summary

A modification of the Farrow structure with reduced computational complexity.
Compared to a conventional design, the impulse response is broken into a higher number of segments. Interpolation accuracy is achieved with a lower polynomial order, requiring fewer multiplications per output sample at the expense of a higher overall number of coefficients.

Example code

This code snippet provides a Matlab / Octave implementation.
And here is the same in C, with explicit sample-per-sample calculation that allows varying the output rate even during operation (the Matlab version is vectorized).

Background

A Farrow structure resamples a signal at an arbitrary, possibly time-varying sampling rate. It utilizes a piecewise polynomial approximation of a continuous-time impulse response.

The proposed variant uses multiple segments per tap instead of one. This may allow to achieve the same accuracy with a lower order polynomial.

Note:

The performance of a Farrow resampler depends mainly on

• The ideal impulse response itself (filter prototype, cutoff frequency, steepness, far-off rejection, limitations from finite duration / limited number of taps)
• The accuracy of the polynomial approximation to the ideal impulse response

The proposed bank switching can improve the approximation accuracy, but the approximation can obviously not outperform the ideal impulse response. In other words, any attempt to improve performance by better approximation accuracy of the impulse response is futile, when the ideal impulse response itself is the limiting factor.

Concept

"Bank-switching" breaks the interpolation segments into smaller pieces.

Fig. 1 shows an example for an impulse response implemented in a conventional Farrow resampler.
Each segment corresponds to one sample of the input signal at a time. The resampler interpolates the impulse response at the sample duration, multiplies with the sample sample and sums the resulting product over all taps at the output.
To calculate the next output sample, the input stream is shifted, for example by 1/3 sample for an output rate that is 3x higher than the input rate. Either a sample stays within its impulse response segment, or it moves to the next tap (segment) by shifting the delay line.

Since the shape of an impulse response can be rather complex over the duration of one segment, a high-order polynomial is required to approximate it with the required accuracy. The arrows in Fig. 1 point out an example segment.

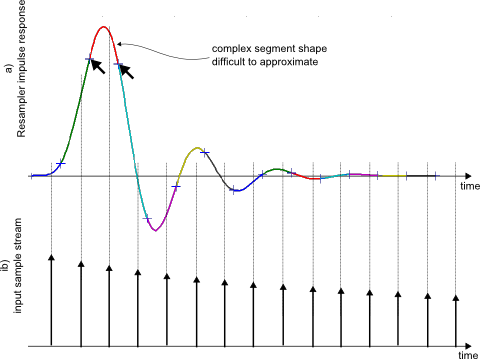
^{Fig.1: Resampler impulse response segments (a) and input signal (b)}

The proposed structure breaks each segment of the impulse response into n sub-segments. This is shown in Fig. 2, with n=2. Since segments become shorter, an accurate approximation can be achieved with a lower-order polynomial.

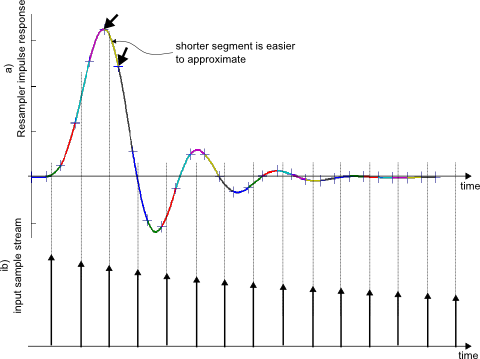
^{Fig.2: Resampler impulse response broken into sub-segments (a) and input signal (b)}

Only every second impulse response segment contributes to the output signal at any given time. Therefore, the number of taps remains unchanged. The interpolator can use bank-switching between alternative polynomial coefficient sets in each tap.

Similarity with polyphase FIR upsampler

The bank-switching concept can be understood in terms of a conventional polyphase FIR interpolator, which is recalled below:

:

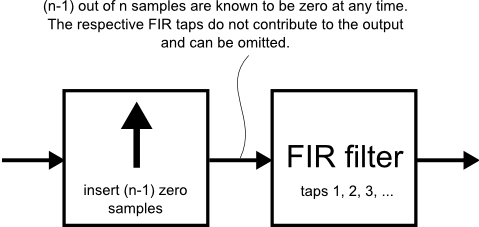^{Fig.3: Interpolation using FIR filter}

As shown in Fig. 3, interpolation by an integer factor n can be performed by inserting (n-1) zero samples and subsequent FIR filtering.
Zero samples do not contribute to the output of the FIR filter and their location in time is always known. Therefore, the structure can be rearranged into the polyphase arrangement in Fig. 4. The term "polyphase" highlights that each coefficient bank generates a different "phase" of the signal, that is, a replica that is delayed by a varying amount.

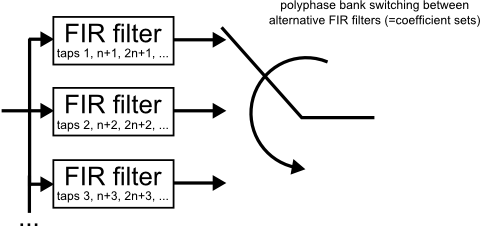
^{Fig.4: Polyphase FIR interpolator}

Instead of fixed FIR coefficients in Fig. 4, the bank-switched Farrow interpolator uses polynomial interpolation (Fig. 5).

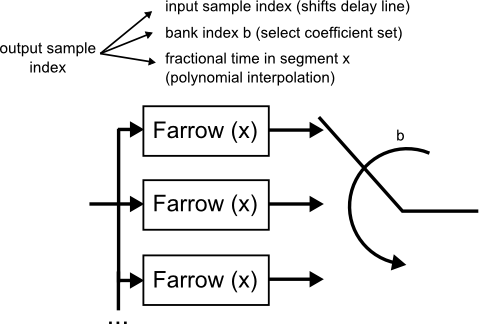
^{Fig.5: Bank-switched Farrow structure}

The time instant of each output sample is split into:

• A first integer part that corresponds to the position in the input stream. A change results in shifting the delay line and processing one (or more) new input samples.
• A second integer part that determines the coefficient bank
• A fractional part that interpolates each bank's impulse response segment.

The calculation is explicitly written out in the C implementation.

Efficient use

A Farrow interpolator that requires 3^rd or higher approximation order may be a good candidate for bank switching. Reducing 2^nd order to linear is usually not practical, since the number of sub-segments needed to maintain accuracy grows too large. These numbers should be taken with caution, since accuracy requirements may differ by several orders of magnitudes, depending on the application.
In any case, some trial-and-error with alternative designs may be useful to find the best solution. Your mileage may vary.

 

Rate this article:
posted by Markus Nentwig
Markus received his Dipl. Ing. degree in electrical engineering / communications in 1999. Work interests include RF transceiver system design, implementation, modeling and verification. He works as senior architect for Renesas Mobile Europe in Finland.

Previous post by Markus Nentwig: A multiuser waterfilling algorithm
Next post by Markus Nentwig: Design study: 1:64 interpolating pulse shaping FIR
all articles by Markus Nentwig

Would you like to be notified by email when Markus Nentwig publishes a new blog?

  

There are no comments yet!