Free Books
   Free Books    Introduction to Digital Filters  

Quality Factor (Q)

The quality factor (Q) of a two-pole resonator is defined by [20, p. 184]

$\displaystyle Q \isdef \frac{\omega_0}{2\alpha} \protect$ (E.7)

where $ \omega_0$ and $ \alpha$ are parameters of the resonator transfer function

$\displaystyle H(s) = g\frac{s}{s^2 + 2\alpha s + \omega_0^2}. \protect$ (E.8)

Note that Q is defined in the context of continuous-time resonators, so the transfer function $ H(s)$ is the Laplace transform (instead of the z transform) of the continuous (instead of discrete-time) impulse-response $ h(t)$. An introduction to Laplace-transform analysis appears in Appendix D. The parameter $ \alpha$ is called the damping constant (or ``damping factor'') of the second-order transfer function, and $ \omega_0$ is called the resonant frequency [20, p. 179]. The resonant frequency $ \omega_0$ coincides with the physical oscillation frequency of the resonator impulse response when the damping constant $ \alpha$ is zero. For light damping, $ \omega_0$ is approximately the physical frequency of impulse-response oscillation ($ 2\pi$ times the zero-crossing rate of sinusoidal oscillation under an exponential decay). For larger damping constants, it is better to use the imaginary part of the pole location as a definition of resonance frequency (which is exact in the case of a single complex pole). (See §B.6 for a more complete discussion of resonators, in the discrete-time case.)

By the quadratic formula, the poles of the transfer function $ H(s)$ are given by

$\displaystyle p = -\alpha \pm \sqrt{\alpha^2 - \omega_0^2} \isdef -\alpha \pm \alpha_d . \protect$ (E.9)

Therefore, the poles are complex only when $ Q>1/2$. Since real poles do not resonate, we have $ Q>1/2$ for any resonator. The case $ Q=1/2$ is called critically damped, while $ Q<1/2$ is called overdamped. A resonator ($ Q>1/2$) is said to be underdamped, and the limiting case $ Q=\infty$ is simply undamped.

Relating to the notation of the previous section, in which we defined one of the complex poles as $ p\isdef \sigma_p+j\omega_p$, we have

$\displaystyle \sigma_p$ $\displaystyle =$ $\displaystyle -\alpha$ (E.10)
$\displaystyle \omega_p$ $\displaystyle =$ $\displaystyle \sqrt{\omega_0-\alpha^2}.$ (E.11)

For resonators, $ \omega_p$ coincides with the classically defined quantity [20, p. 624]

$\displaystyle \omega_d \isdef \omega_p = \sqrt{\omega_0^2 -\alpha^2} = \frac{\alpha_d}{j}. $

Since the imaginary parts of the complex resonator poles are $ \pm\omega_d$, the zero-crossing rate of the resonator impulse response is $ \omega_d/\pi$ crossings per second. Moreover, $ \omega_d$ is very close to the peak-magnitude frequency in the resonator amplitude response. If we eliminate the negative-frequency pole, $ \omega_d/\pi$ becomes exactly the peak frequency. In other words, as a measure of resonance peak frequency, $ \omega_d$ only neglects the interaction of the positive- and negative-frequency resonance peaks in the frequency response, which is usually negligible except for highly damped, low-frequency resonators. For any amount of damping $ \omega_d/\pi$ gives the impulse-response zero-crossing rate exactly, as is immediately seen from the derivation in the next section.

Decay Time is Q Periods

Another well known rule of thumb is that the $ Q$ of a resonator is the number of ``periods'' under the exponential decay of its impulse response. More precisely, we will show that, for $ Q\gg 1/2$, the impulse response decays by the factor $ e^{-\pi}$ in $ Q$ cycles, which is about 96 percent decay, or -27 dB.

The impulse response corresponding to Eq.$ \,$(E.8) is found by inverting the Laplace transform of the transfer function $ H(s)$. Since it is only second order, the solution can be found in many tables of Laplace transforms. Alternatively, we can break it up into a sum of first-order terms which are invertible by inspection (possibly after rederiving the Laplace transform of an exponential decay, which is very simple). Thus we perform the partial fraction expansion of Eq.$ \,$(E.8) to obtain

$\displaystyle H(s) = \frac{g_1}{s-p_1} + \frac{g_2}{s-p_2} $

where $ p_i$ are given by Eq.$ \,$(E.9), and some algebra gives
$\displaystyle g_1$ $\displaystyle =$ $\displaystyle -g\frac{p_1}{p_2-p_1}$ (E.12)
$\displaystyle g_2$ $\displaystyle =$ $\displaystyle g\frac{p_2}{p_2-p_1}$ (E.13)

as the respective residues of the poles $ p_i$.

The impulse response is thus

$\displaystyle h(t) = g_1 e^{p_1t} + g_2 e^{p_2t}. $

Assuming a resonator, $ Q>1/2$, we have $ p_2 = \overline{p}_1$, where $ p_1=\sigma_p +j\omega_p = -\alpha + j\omega_d$ (using notation of the preceding section), and the impulse response reduces to

$\displaystyle h(t) = g_1\,e^{p_1 t} + \overline{g}_1\,e^{\overline{p}_1 t} = A\,e^{-\alpha t} \cos(\omega_p t + \phi) $

where $ A$ and $ \phi$ are overall amplitude and phase constants, respectively.E.1

We have shown so far that the impulse response $ h(t)$ decays as $ e^{-\alpha t}$ with a sinusoidal radian frequency $ \omega_p=\omega_d$ under the exponential envelope. After Q periods at frequency $ \omega_p$, time has advanced to

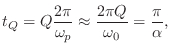
$\displaystyle t_Q = Q\frac{2\pi}{\omega_p} \approx \frac{2\pi Q}{\omega_0} = \frac{\pi}{\alpha}, $

where we have used the definition Eq.$ \,$(E.7) $ Q\isdef \omega_0/(2\alpha)$. Thus, after $ Q$ periods, the amplitude envelope has decayed to

$\displaystyle e^{-\alpha t_Q} = e^{-\pi} \approx 0.043\dots $

which is about 96 percent decay. The only approximation in this derivation was

$\displaystyle \omega_p = \sqrt{\omega_0^2 - \alpha^2} \approx \omega_0 $

which holds whenever $ \alpha\ll\omega_0$, or $ Q\gg 1/2$.

Q as Energy Stored over Energy Dissipated

Yet another meaning for $ Q$ is as follows [20, p. 326]

$\displaystyle Q = 2\pi\frac{\hbox{Stored Energy}}{\hbox{Energy Dissipated in One Cycle}} $

where the resonator is freely decaying (unexcited).

Proof. The total stored energy at time $ t$ is equal to the total energy of the remaining response. After an impulse at time 0, the stored energy in a second-order resonator is

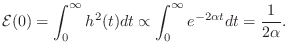
$\displaystyle {\cal E}(0) = \int_0^\infty h^2(t)dt \propto \int_0^\infty e^{-2\alpha t}dt = \frac{1}{2\alpha}. $

The energy dissipated in the first period $ P = 2\pi/\omega_p$ is $ {\cal E}(0)-{\cal E}(P)$, where

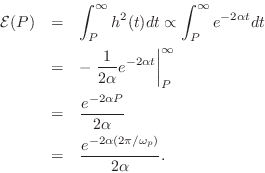
\begin{eqnarray*} {\cal E}(P) &=& \int_P^\infty h^2(t)dt \propto \int_P^\infty e... ...}}{2\alpha}\\ &=& \frac{e^{-2\alpha (2\pi/\omega_p)}}{2\alpha}. \end{eqnarray*}

Assuming $ Q\gg 1/2$ as before, $ \omega_p\approx\omega_0$ so that

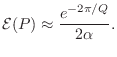
$\displaystyle {\cal E}(P) \approx \frac{e^{-2\pi/Q}}{2\alpha}. $

Assuming further that $ Q\gg 2\pi$, we obtain

$\displaystyle {\cal E}(0)-{\cal E}(P) \approx \frac{1}{2\alpha} \left(1-e^{-\frac{2\pi}{Q}}\right) \approx \frac{1}{2\alpha}\frac{2\pi}{Q}. $

This is the energy dissipated in one cycle. Dividing this into the total stored energy at time zero, $ {\cal E}(0)=1/(2\alpha)$, gives

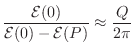
$\displaystyle \frac{{\cal E}(0)}{{\cal E}(0)-{\cal E}(P)} \approx \frac{Q}{2\pi} $

whence

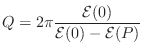
$\displaystyle Q = 2\pi \frac{{\cal E}(0)}{{\cal E}(0)-{\cal E}(P)} $

as claimed. Note that this rule of thumb requires $ Q\gg 2\pi$, while the one of the previous section only required $ Q\gg 1/2$.

Next Section:
Analog Allpass Filters
Previous Section:
Relating Pole Radius to Bandwidth