DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

The Biquad Allpass Section

The general biquad transfer function was given in Eq.$ \,$(B.8) to be

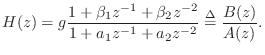
$\displaystyle H(z) = g \frac{1 + \beta_1 z^{-1}+ \beta_2 z^{-2}}{1 + a_1 z^{-1}+ a_2 z^{-2}} \isdef \frac{B(z)}{A(z)}. $

To specialize this to a second-order unity-gain allpass filter, we require

$\displaystyle \left\vert H(e^{j\omega T})\right\vert = 1. $

It is easy to show that, given any monic denominator polynomial $ A(z)$, the numerator $ B(z)$ must be, in the real case,B.3

$\displaystyle B(z) = z^{-2}A(z^{-1}) = a_2 + a_1z^{-1}+ z^{-2}. $

Thus, to obtain an allpass biquad section, the numerator polynomial is simply the ``flip'' of the denominator polynomial. To obtain unity gain, we set $ g=a_2$, $ \beta_1 = a_1/a_2$, and $ \beta_2=1/a_2$.

In terms of the poles and zeros of a filter $ H(z)=B(z)/A(z)$, an allpass filter must have a zero at $ z=1/p$ for each pole at $ z=p$. That is if the denominator $ A(z)$ satisfies $ A(p)=0$, then the numerator polynomial $ B(z)$ must satisfy $ B(1/p)=0$. (Show this in the one-pole case.) Therefore, defining $ B(z) = A(1/z)$ takes care of this property for all roots of $ A(z)$ (all poles). However, since we prefer that $ B(z)$ be a polynomial in $ z^{-1}$, we define $ B(z) = z^{-N}A(1/z)$, where $ N$ is the order of $ A(z)$ (the number of poles). $ B(z)$ is then the flip of $ A(z)$.

For further discussion and examples of allpass filters (including muli-input, multi-output allpass filters), see Appendix C. Analog allpass filters are defined and discussed in §E.8.

Next Section:
Allpass Filter Design
Previous Section:
Biquad Software Implementations