Elementary Zero-Phase Filter Examples

Free Books Introduction to Digital Filters

A practical zero-phase filter was illustrated in Figures 10.1 and 10.2. Some simple general cases are as follows:

The trivial (non-)filter 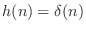$h(n)=\delta(n)$ has frequency response 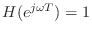$H(e^{j\omega T})=1$ , which is zero phase for all $\omega$ .
Every second-order zero-phase FIR filter has an impulse response of the form

$\displaystyle h(n) \eqsp b_{1}\delta(n+1) + b_0\delta(n) + b_1 \delta(n-1),$
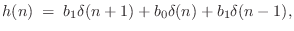
where the coefficients 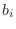are assumed real. The transfer function of the general, second-order, real, zero-phase filter is

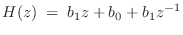$\displaystyle H(z) \eqsp b_{1}z + b_0 + b_1 z^{-1}$
and the frequency response is

$\displaystyle H(e^{j\omega T}) \eqsp b_{1}e^{j\omega T}+ b_0 + b_1 e^{-j\omega T}\eqsp b_0 + 2 b_1 \cos(\omega T)$
which is real for all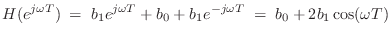 $\omega$ .
Extending the previous example, every order 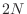zero-phase real FIR filter has an impulse response of the form

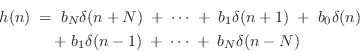
$\begin{eqnarray*} \lefteqn{ h(n) \eqsp b_{N}\delta(n+N) \;+\; \cdots \;+\; b_{... ...ots & & \;+\; b_1 \delta(n-1) \;+\; \cdots \;+\; b_N\delta(n-N) \end{eqnarray*}$

and frequency response

$\displaystyle H(e^{j\omega T}) \eqsp b_0 \;+\; 2 \sum_{k=1}^N b_k \cos(k\omega T)$
which is clearly real whenever the coefficients 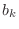are real.
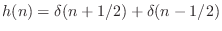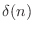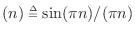There is no first-order (length 2) zero-phase filter, because, to be even, its impulse response would have to be proportional to $h(n)=\delta(n+1/2) + \delta(n-1/2)$ . Since the bandlimited digital impulse signal $\delta (n)$ is ideally interpolated using bandlimited interpolation [91,84], giving samples of sinc $(n)\isdeftext \sin(\pi n)/(\pi n)$ --the unit-amplitude sinc function having zero-crossings on the integers, we see that sampling on the integers yields an IIR filter:

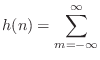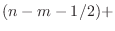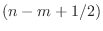
$\displaystyle h(n) = \sum_{m=-\infty}^{\infty}$ sinc $\displaystyle (n-m-1/2) +$ sinc $\displaystyle (n-m+1/2)$
Similarly, there are no odd-order (even-length) zero-phase filters.