DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Group Delay Examples in Matlab

Figure 7.6 compares the group delay responses for a number of classic lowpass filters, including the example of Fig.7.2. The matlab code is listed in Fig.7.5. See, e.g., Parks and Burrus [64] for a discussion of Butterworth, Chebyshev, and Elliptic Function digital filter design. See also §I.2 for details on the Butterworth case. The various types may be summarized as follows:

  • Butterworth filters are maximally flat in middle of the passband.
  • Chebyshev Type I filters are ``equiripple'' in the passband and ``Butterworth'' in the stopband.
  • Chebyshev Type II filters are ``Butterworth'' in the passband and equiripple in the stopband.
  • Elliptic function filters are equiripple in both the passband and stopband.
Here, ``equiripple'' means ``equal ripple''; that is, the error oscillates with equal peak magnitudes across the band. An equiripple error characterizes optimality in the Chebyshev sense [64,78].

As Fig.7.6.4 indicates, and as is well known, the Butterworth filter has the flattest group delay curve (and most gentle transition from passband to stopband) for the four types compared. The elliptic function filter has the largest amount of ``delay distortion'' near the cut-off frequency (passband edge frequency). Fundamentally, the more abrupt the transition from passband to stopband, the greater the delay-distortion across that transition, for any minimum-phase filter. (Minimum-phase filters are introduced in Chapter 11.) The delay-distortion can be compensated by delay equalization, i.e., adding delay at other frequencies in order approach an overall constant group delay versus frequency. Delay equalization is typically carried out using an allpass filter (defined in §B.2) in series with the filter to be delay-equalized [1].

Figure 7.5: Program (matlab) for comparing the amplitude and group-delay responses of four classic lowpass filter types: Butterworth, Chebyshev Type I, Chebyshev Type II, and Elliptic Function.
  
[Bb,Ab] = butter(4,0.5); % order 4, cutoff at 0.5 * pi
Hb=freqz(Bb,Ab);
Db=grpdelay(Bb,Ab);

[Bc1,Ac1] = cheby1(4,1,0.5); % 1 dB passband ripple
Hc1=freqz(Bc1,Ac1);
Dc1=grpdelay(Bc1,Ac1);

[Bc2,Ac2] = cheby2(4,20,0.5); % 20 dB stopband attenuation
Hc2=freqz(Bc2,Ac2);
Dc2=grpdelay(Bc2,Ac2);

[Be,Ae] = ellip(4,1,20,0.5);  % like cheby1 + cheby2
He=freqz(Be,Ae);
[De,w]=grpdelay(Be,Ae);

figure(1); plot(w,abs([Hb,Hc1,Hc2,He])); grid('on');
xlabel('Frequency (rad/sample)'); ylabel('Gain');
legend('butter','cheby1','cheby2','ellip');
saveplot('../eps/grpdelaydemo1.eps');

figure(2); plot(w,[Db,Dc1,Dc2,De]); grid('on');
xlabel('Frequency (rad/sample)'); ylabel('Delay (samples)');
legend('butter','cheby1','cheby2','ellip');
saveplot('../eps/grpdelaydemo2.eps');

Figure 7.6: Comparison of amplitude and group-delay responses for classic lowpass-filter types Butterworth, Chebyshev Type I, Chebyshev Type II, and Elliptic Function. Plots generated by Octave 2.9.7 and octave-forge 2006-07-09.
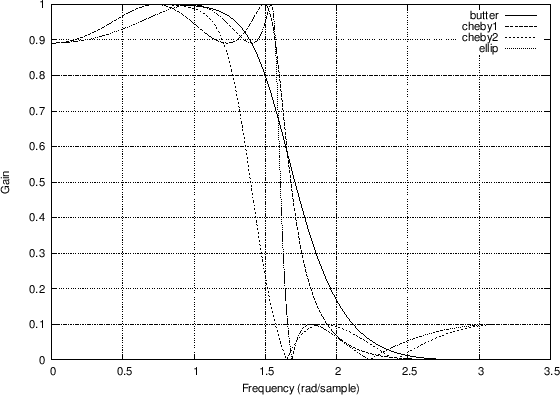
\includegraphics{eps/grpdelaydemo1}

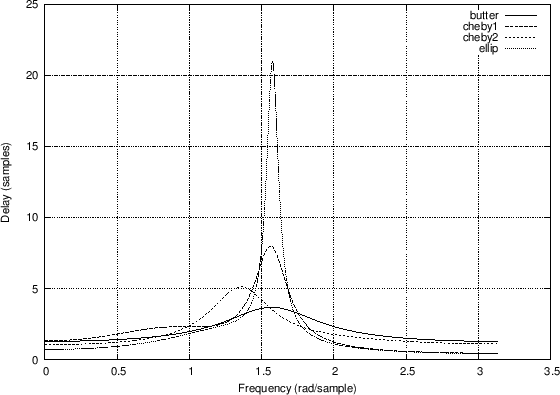
\includegraphics{eps/grpdelaydemo2}
Group Delays

Next Section:
Vocoder Analysis
Previous Section:
Group Delay