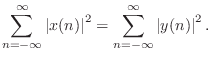DSPRelated.com
Free Books
   Free Books    Introduction to Digital Filters  

Allpass Filter Sections

The allpass filter passes all frequencies with equal gain. This is in contrast with a lowpass filter, which passes only low frequencies, a highpass which passes high-frequencies, and a bandpass filter which passes an interval of frequencies. An allpass filter may have any phase response. The only requirement is that its amplitude response be constant. Normally, this constant is $ \left\vert H(e^{j\omega T})\right\vert=1$.

From a physical modeling point of view, a unity-gain allpass filter models a lossless system in the sense that it preserves signal energy. Specifically, if $ x(n)$ denotes the input to an allpass filter $ H(z)$, and if $ y(n)$ denotes its output, then we have

$\displaystyle \sum_{n=-\infty}^\infty \left\vert x(n)\right\vert^2 = \sum_{n=-\infty}^\infty \left\vert y(n)\right\vert^2. \protect$ (B.9)

This equation says that the total energy out equals the total energy in. No energy was created or destroyed by the filter. All an allpass filter can do is delay the sinusoidal components of a signal by differing amounts.

Appendix C proves that Eq.$ \,$(B.9) holds if and only if

$\displaystyle \left\vert H(e^{j\omega T})\right\vert = 1, \quad \forall \omega. $

That is, a filter $ H(z)$ is lossless if and only if it is an allpass filter having a gain of $ 1$ at every frequency $ \omega$.

The Biquad Allpass Section

The general biquad transfer function was given in Eq.$ \,$(B.8) to be

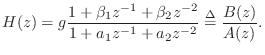
$\displaystyle H(z) = g \frac{1 + \beta_1 z^{-1}+ \beta_2 z^{-2}}{1 + a_1 z^{-1}+ a_2 z^{-2}} \isdef \frac{B(z)}{A(z)}. $

To specialize this to a second-order unity-gain allpass filter, we require

$\displaystyle \left\vert H(e^{j\omega T})\right\vert = 1. $

It is easy to show that, given any monic denominator polynomial $ A(z)$, the numerator $ B(z)$ must be, in the real case,B.3

$\displaystyle B(z) = z^{-2}A(z^{-1}) = a_2 + a_1z^{-1}+ z^{-2}. $

Thus, to obtain an allpass biquad section, the numerator polynomial is simply the ``flip'' of the denominator polynomial. To obtain unity gain, we set $ g=a_2$, $ \beta_1 = a_1/a_2$, and $ \beta_2=1/a_2$.

In terms of the poles and zeros of a filter $ H(z)=B(z)/A(z)$, an allpass filter must have a zero at $ z=1/p$ for each pole at $ z=p$. That is if the denominator $ A(z)$ satisfies $ A(p)=0$, then the numerator polynomial $ B(z)$ must satisfy $ B(1/p)=0$. (Show this in the one-pole case.) Therefore, defining $ B(z) = A(1/z)$ takes care of this property for all roots of $ A(z)$ (all poles). However, since we prefer that $ B(z)$ be a polynomial in $ z^{-1}$, we define $ B(z) = z^{-N}A(1/z)$, where $ N$ is the order of $ A(z)$ (the number of poles). $ B(z)$ is then the flip of $ A(z)$.

For further discussion and examples of allpass filters (including muli-input, multi-output allpass filters), see Appendix C. Analog allpass filters are defined and discussed in §E.8.

Allpass Filter Design

There is a fairly large literature thread on the topic of allpass filter design. Generally, they fall into two main categories: parametric and nonparametric methods. Parametric methods can produce allpass filters with optimal group-delay characteristics [42,41]. Nonparametric methods, while suboptimal, can design very large-order allpass filters, and errors can usually be made arbitrarily small by increasing the order [100,70,1], [78, pp. 60,172]. In music applications, it is usually the case that the ``optimality'' criterion is unknown because it depends on aspects of sound perception (see, for example, [35,72]). As a result, perceptually weighted nonparametric methods can often outperform optimal parametric methods in terms of cost/performance. For a nonparametric method that can design very high-order allpass filters according to highly flexible criteria, see [1].

Next Section:
DC Blocker
Previous Section:
Elementary Filter Sections