Maximum Phase Filters
The opposite of minimum phase is maximum phase:
For example, every stable allpass filter (§B.2) is a maximum-phase filter, because its transfer function can be written as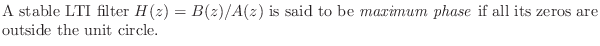
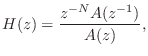
If zeros of ![]() occur both inside and outside the unit circle, the
filter is said to be a mixed-phase filter. Note that zeros on
the unit circle are neither minimum nor maximum phase according to our
definitions. Since poles on the unit circle are sometimes called
``marginally stable,'' we could say that zeros on the unit circle are
``marginally minimum and/or maximum phase'' for consistency. However,
such a term does not appear to be very useful. When pursuing
minimum-phase filter design (see §11.7), we will
find that zeros on the unit circle must be treated separately.
occur both inside and outside the unit circle, the
filter is said to be a mixed-phase filter. Note that zeros on
the unit circle are neither minimum nor maximum phase according to our
definitions. Since poles on the unit circle are sometimes called
``marginally stable,'' we could say that zeros on the unit circle are
``marginally minimum and/or maximum phase'' for consistency. However,
such a term does not appear to be very useful. When pursuing
minimum-phase filter design (see §11.7), we will
find that zeros on the unit circle must be treated separately.
If ![]() is order
is order ![]() and minimum phase, then
and minimum phase, then
![]() is
maximum phase, and vice versa. To restate this in the time domain, if
is
maximum phase, and vice versa. To restate this in the time domain, if
![]() is a minimum-phase FIR sequence of
length
is a minimum-phase FIR sequence of
length ![]() , then
SHIFT
, then
SHIFT![]() FLIP
FLIP![]() is a maximum-phase sequence.
In other words, time reversal inverts the locations of all
zeros, thereby ``reflecting'' them across the unit circle in a manner
that does not affect spectral magnitude. Time reversal is followed by
a shift in order to obtain a causal result, but this is not required:
Adding a pure delay to a maximum-phase filter (
is a maximum-phase sequence.
In other words, time reversal inverts the locations of all
zeros, thereby ``reflecting'' them across the unit circle in a manner
that does not affect spectral magnitude. Time reversal is followed by
a shift in order to obtain a causal result, but this is not required:
Adding a pure delay to a maximum-phase filter (
![]() ) gives a new maximum-phase filter with the same amplitude
response (and order increased by 1).
) gives a new maximum-phase filter with the same amplitude
response (and order increased by 1).
Example
It is easy to classify completely all first-order FIR filters:
Next Section:
Minimum Phase Means Fastest Decay
Previous Section:
Minimum-Phase Polynomials



















