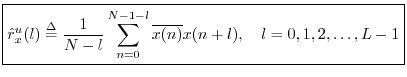Free Books    Mathematics of the DFT  

Correlation Analysis

The correlation operator (defined in §7.2.5) plays a major role in statistical signal processing. For a proper development, see, e.g., [27,33,65]. This section introduces only some of the most basic elements of statistical signal processing in a simplified manner, with emphasis on illustrating applications of the DFT.

Cross-Correlation


Definition: The circular cross-correlation of two signals $ x$ and $ y$ in $ {\bf C}^N$ may be defined by

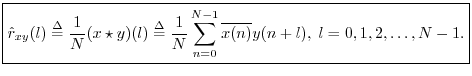
$\displaystyle \zbox {{\hat r}_{xy}(l) \isdef \frac{1}{N}(x\star y)(l) \isdef \frac{1}{N}\sum_{n=0}^{N-1}\overline{x(n)} y(n+l), \; l=0,1,2,\ldots,N-1.} $

(Note that the ``lag'' $ l$ is an integer variable, not the constant $ 1$.) The DFT correlation operator `$ \star$' was first defined in §7.2.5.

The term ``cross-correlation'' comes from statistics, and what we have defined here is more properly called a ``sample cross-correlation.'' That is, $ {\hat r}_{xy}(l)$ is an estimator8.8 of the true cross-correlation $ r_{xy}(l)$ which is an assumed statistical property of the signal itself. This definition of a sample cross-correlation is only valid for stationary stochastic processes, e.g., ``steady noises'' that sound unchanged over time. The statistics of a stationary stochastic process are by definition time invariant, thereby allowing time-averages to be used for estimating statistics such as cross-correlations. For brevity below, we will typically not include ``sample'' qualifier, because all computational methods discussed will be sample-based methods intended for use on stationary data segments.

The DFT of the cross-correlation may be called the cross-spectral density, or ``cross-power spectrum,'' or even simply ``cross-spectrum'':

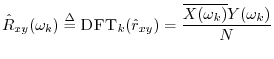
$\displaystyle {\hat R}_{xy}(\omega_k) \isdef \hbox{\sc DFT}_k({\hat r}_{xy}) = \frac{\overline{X(\omega_k)}Y(\omega_k)}{N} $

The last equality above follows from the correlation theorem (§7.4.7).

Unbiased Cross-Correlation

Recall that the cross-correlation operator is cyclic (circular) since $ n+l$ is interpreted modulo $ N$. In practice, we are normally interested in estimating the acyclic cross-correlation between two signals. For this (more realistic) case, we may define instead the unbiased cross-correlation

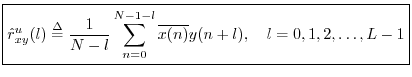
$\displaystyle \zbox {{\hat r}^u_{xy}(l) \isdef \frac{1}{N-l}\sum_{n=0}^{N-1-l} \overline{x(n)} y(n+l),\quad l = 0,1,2,\ldots,L-1} $

where we choose $ L\ll N$ (e.g., $ L\approx\sqrt{N}$) in order to have enough lagged products $ \overline{x(n)} y(n+l)$ at the highest lag $ L-1$ so that a reasonably accurate average is obtained. Note that the summation stops at $ n=N-l-1$ to avoid cyclic wrap-around of $ n$ modulo $ N$. The term ``unbiased'' refers to the fact that the expected value8.9[33] of $ {\hat r}^u_{xy}(l)$ is the true cross-correlation $ r_{xy}(l)$ of $ x$ and $ y$ (assumed to be samples from stationary stochastic processes).

An unbiased acyclic cross-correlation may be computed faster via DFT (FFT) methods using zero padding:

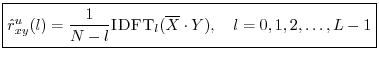
$\displaystyle \zbox {{\hat r}^u_{xy}(l) = \frac{1}{N-l}\hbox{\sc IDFT}_l(\overline{X}\cdot Y), \quad l = 0,1,2,\ldots,L-1} $

where

\begin{eqnarray*} X &=& \hbox{\sc DFT}[\hbox{\sc CausalZeroPad}_{N+L-1}(x)]\\ Y &=& \hbox{\sc DFT}[\hbox{\sc CausalZeroPad}_{N+L-1}(y)]. \end{eqnarray*}

Note that $ x$ and $ y$ belong to $ {\bf C}^N$ while $ X$ and $ Y$ belong to $ {\bf C}^{N+L-1}$. The zero-padding may be causal (as defined in §7.2.8) because the signals are assumed to be be stationary, in which case all signal statistics are time-invariant. As usual when embedding acyclic correlation (or convolution) within the cyclic variant given by the DFT, sufficient zero-padding is provided so that only zeros are ``time aliased'' (wrapped around in time) by modulo indexing.

Cross-correlation is used extensively in audio signal processing for applications such as time scale modification, pitch shifting, click removal, and many others.

Autocorrelation

The cross-correlation of a signal with itself gives its autocorrelation:

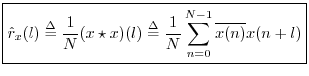
$\displaystyle \zbox {{\hat r}_x(l) \isdef \frac{1}{N}(x\star x)(l) \isdef \frac{1}{N}\sum_{n=0}^{N-1}\overline{x(n)} x(n+l)} $

The autocorrelation function is Hermitian:

$\displaystyle {\hat r}_x(-l) = \overline{{\hat r}_x(l)} $

When $ x$ is real, its autocorrelation is real and even (symmetric about lag zero).

The unbiased cross-correlation similarly reduces to an unbiased autocorrelation when $ x\equiv y$:

$\displaystyle \zbox {{\hat r}^u_x(l) \isdef \frac{1}{N-l}\sum_{n=0}^{N-1-l} \overline{x(n)} x(n+l),\quad l = 0,1,2,\ldots,L-1} \protect$ (8.2)

The DFT of the true autocorrelation function $ r_x(n)\in{\bf R}^N$ is the (sampled) power spectral density (PSD), or power spectrum, and may be denoted

$\displaystyle R_x(\omega_k) \isdef \hbox{\sc DFT}_k(r_x). $

The complete (not sampled) PSD is $ R_x(\omega) \isdef \hbox{\sc DTFT}_k(r_x)$, where the DTFT is defined in Appendix B (it's just an infinitely long DFT). The DFT of $ {\hat r}_x$ thus provides a sample-based estimate of the PSD:8.10

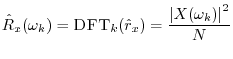
$\displaystyle {\hat R}_x(\omega_k)=\hbox{\sc DFT}_k({\hat r}_x) = \frac{\left\vert X(\omega_k)\right\vert^2}{N} $

We could call $ {\hat R}_x(\omega_k)$ a ``sampled sample power spectral density''.

At lag zero, the autocorrelation function reduces to the average power (mean square) which we defined in §5.8:

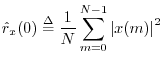
$\displaystyle {\hat r}_x(0) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\left\vert x(m)\right\vert^2 % \isdef \Pscr_x^2 $

Replacing ``correlation'' with ``covariance'' in the above definitions gives corresponding zero-mean versions. For example, we may define the sample circular cross-covariance as

$\displaystyle \zbox {{\hat c}_{xy}(n) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\overline{[x(m)-\mu_x]} [y(m+n)-\mu_y].} $

where $ \mu_x$ and $ \mu_y$ denote the means of $ x$ and $ y$, respectively. We also have that $ {\hat c}_x(0)$ equals the sample variance of the signal $ x$:

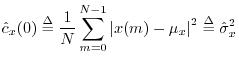
$\displaystyle {\hat c}_x(0) \isdef \frac{1}{N}\sum_{m=0}^{N-1}\left\vert x(m)-\mu_x\right\vert^2 \isdef {\hat \sigma}_x^2 $

Matched Filtering

The cross-correlation function is used extensively in pattern recognition and signal detection. We know from Chapter 5 that projecting one signal onto another is a means of measuring how much of the second signal is present in the first. This can be used to ``detect'' the presence of known signals as components of more complicated signals. As a simple example, suppose we record $ x(n)$ which we think consists of a signal $ s(n)$ that we are looking for plus some additive measurement noise $ e(n)$. That is, we assume the signal model $ x(n)=s(n)+e(n)$. Then the projection of $ x$ onto $ s$ is (recalling §5.9.9)

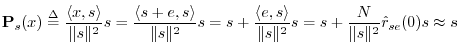
$\displaystyle {\bf P}_s(x) \isdef \frac{\left<x,s\right>}{\Vert s\Vert^2} s = \... ...}{\Vert s\Vert^2} s = s + \frac{N}{\Vert s\Vert^2} {\hat r}_{se}(0)s \approx s $

since the projection of random, zero-mean noise $ e$ onto $ s$ is small with probability one. Another term for this process is matched filtering. The impulse response of the ``matched filter'' for a real signal $ s$ is given by $ \hbox{\sc Flip}(s)$.8.11 By time-reversing $ s$, we transform the convolution implemented by filtering into a sliding cross-correlation operation between the input signal $ x$ and the sought signal $ s$. (For complex known signals $ s$, the matched filter is $ \hbox{\sc Flip}(\overline{s})$.) We detect occurrences of $ s$ in $ x$ by detecting peaks in $ {\hat r}_{sx}(l)$.

In the same way that FFT convolution is faster than direct convolution (see Table 7.1), cross-correlation and matched filtering are generally carried out most efficiently using an FFT algorithm (Appendix A).

FIR System Identification

Estimating an impulse response from input-output measurements is called system identification, and a large literature exists on this topic (e.g., [39]).

Cross-correlation can be used to compute the impulse response $ h(n)$ of a filter from the cross-correlation of its input and output signals $ x(n)$ and $ y = h\ast x$, respectively. To see this, note that, by the correlation theorem,

$\displaystyle x\star y \;\longleftrightarrow\;\overline{X}\cdot Y = \overline{X}\cdot (H\cdot X) = H\cdot\left\vert X\right\vert^2. $

Therefore, the frequency response equals the input-output cross-spectrum divided by the input power spectrum:

$\displaystyle H = \frac{\overline{X}\cdot Y}{\left\vert X\right\vert^2} = \frac{{\hat R}_{xy}}{{\hat R}_{xx}} $

where multiplication and division of spectra are defined pointwise, i.e., $ H(\omega_k) = \overline{X(\omega_k)}\cdot Y(\omega_k)/\vert X(\omega_k)\vert^2$. A Matlab program illustrating these relationships is listed in Fig.8.13.

Figure 8.13: FIR system identification example in matlab.
  
% sidex.m - Demonstration of the use of FFT cross-
% correlation to compute the impulse response
% of a filter given its input and output.
% This is called "FIR system identification".

Nx = 32; % input signal length
Nh = 10; % filter length
Ny = Nx+Nh-1; % max output signal length
% FFT size to accommodate cross-correlation:
Nfft = 2^nextpow2(Ny); % FFT wants power of 2

x = rand(1,Nx); % input signal = noise
%x = 1:Nx; 	% input signal = ramp
h = [1:Nh]; 	% the filter
xzp = [x,zeros(1,Nfft-Nx)]; % zero-padded input
yzp = filter(h,1,xzp); % apply the filter
X = fft(xzp);   % input spectrum
Y = fft(yzp);   % output spectrum
Rxx = conj(X) .* X; % energy spectrum of x
Rxy = conj(X) .* Y; % cross-energy spectrum
Hxy = Rxy ./ Rxx;   % should be the freq. response
hxy = ifft(Hxy);    % should be the imp. response

hxy(1:Nh) 	    % print estimated impulse response
freqz(hxy,1,Nfft);  % plot estimated freq response

err = norm(hxy - [h,zeros(1,Nfft-Nh)])/norm(h);
disp(sprintf(['Impulse Response Error = ',...
	'%0.14f%%'],100*err));

err = norm(Hxy-fft([h,zeros(1,Nfft-Nh)]))/norm(h);
disp(sprintf(['Frequency Response Error = ',...
	'%0.14f%%'],100*err));

Next Section:
Power Spectral Density Estimation
Previous Section:
Filters and Convolution